 |
A G. 774. feladat (2022. március) |
G. 774. Az alábbi diagramon a Duna felszíni sebességprofilja látható az Erzsébet-hídnál 2018. március 10-én. A vízszintes tengelyen a bal parttól mért távolság (s) látható méterben, a függőleges tengelyen a Duna sebessége (v) m/s-ban. A mellékelt táblázatban találhatóak a mért adatok.
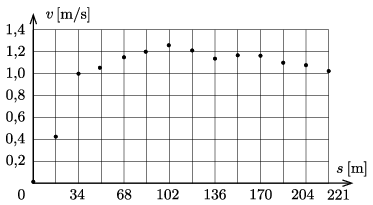
| s [m] | v [m/s] | s [m] | v [m/s] |
| 0 | 0,00 | 119 | 1,21 |
| 17 | 0,41 | 136 | 1,14 |
| 34 | 1,00 | 153 | 1,17 |
| 51 | 1,05 | 170 | 1,17 |
| 68 | 1,15 | 187 | 1,10 |
| 85 | 1,19 | 204 | 1,07 |
| 102 | 1,26 | 221 | 1,02 |
Becsüljük meg, hogy hány méterrel sodorna le a Duna, ha a bal parttól a partra mindig merőlegesen 1 m/s sebességgel eveznénk át egy, a bal parttól 221 méterre lévő hajóig!
Közli: Csernovszky Zoltán, Budapest
(4 pont)
A beküldési határidő 2022. április 19-én LEJÁRT.
Megoldás. A becslést többféle módon is elvégezhetjük. A megadott sebességprofil grafikonon látszik, hogy az első 34 méteren a folyó sebessége nagyjából egyenletesen növekszik 0-ról 1 m/s-ra, ezen a szakaszon tehát számolhatunk 0,5 m/s-os átlagsebességgel. Az első 34 méteren, vagyis 34 s alatt a csónak 17 méternyit sodródna lefelé. A mozgás további 221−34=188 méterén a víz sebessége jó közelítéssel állandó 1,1 m/s-nak vehető, a sodródás nagysága tehát 1,1⋅188≈206 méter, a teljes szakaszon pedig összesen kb. 223 m≈220 m. (Ennél pontosabban nincs értelme az eredményt megadni, hiszen a becslésnél használt közelítés ±10 méteres hibát is okozhatott.)
Egy másik eljárás: A táblázatban megadott vi értékeknek páronként képezzük a számtani közepét, és az így kapott
¯vi=vi+vi+12
átlagsebességgel számítjuk ki az i-edik szakaszhoz tartozó di lesodródást. Így a becsült érték:
d=∑idi=(0+0,412+0,41+1,002+1,00+1,052+⋯+1,07+1,022)ms⋅(17 s)≈230 s.
A harmadik eljárás az lehet, hogy a mérési adatokra (számítógép segítségével) egy ,,sima'' görbét illesztünk, és az ezt leíró v(x) függvény integrálját számítjuk ki. Ennek részleteit azonban itt nem tárgyaljuk.
Statisztika:
31 dolgozat érkezett. 4 pontot kapott: Biró Kata, Bocor Gergely, Csilling Dániel, Csóka Péter, Egyházi Godó, Fehérvári Donát, Fercsák Flórián, Földi Albert, Heisz András Botond, Hruby Laura, Jávor Botond, Kiss 668 Benedek, Kiss 987 Barnabás, Kiss Hunor, Klement Tamás, Marosi Botond Máté, Medgyesi Júlia, Nagy 639 Csenge, Richlik Márton, Sós Ádám, Sütő Áron, Téglás Dorka, Toplak Ágnes. 3 pontot kapott: Jacsman Vencel , Jankó Sebestyén, Novák Péter. Nem versenyszerű: 2 dolgozat.
A KöMaL 2022. márciusi fizika feladatai
|
|

