A G. 804. feladat (2023. január)

G. 804. Egy \(\displaystyle 0{,}6~\mathrm{kg/dm}^3\) sűrűségű fahasáb, melynek magassága 40 cm, alapélei pedig 80 cm és 30 cm hosszúak, egy nagy méretű medencében úszik. A hasábot az ábrán látható módon a medence aljához rögzítettük egy rugóval, melynek nyújtatlan hossza 50 cm.

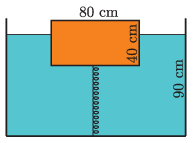
\(\displaystyle a)\) Mennyi látszik ki a hasábból, ha víz mélysége 90 cm és a rugó rugóállandója 1440 N/m?

\(\displaystyle b)\) Legalább mekkora munkavégzés árán lehet a hasábot teljesen a víz felszíne fölé emelni, ha a rugó közben nem szakad el?

(4 pont)

A beküldési határidő 2023. február 15-én LEJÁRT.

Megoldás. A példa szövegében nagy méretű medence szerepel, ami azt jelenti, hogy a hasáb bármilyen mértékű vízbe merülése nem befolyásolja a vízszintet.

\(\displaystyle a)\) Mivel a fahasáb sűrűsége 0,6 kg/\(\displaystyle \rm{dm}^3\), így a rugó hatása nélkül a hasáb 40 cm-es magasságának 60%-a, vagyis 24 cm merülne a vízbe. Ez azt jelenti, hogy ekkor \(\displaystyle 90-24=66\) cm-rel lenne a hasáb alja a medence aljától. A rugó nyújtatlan hossza azonban csak 50 cm, ezért a megnyúlt rugó lejjebb húzza a fahasábot.

Jelöljük a fahasábból kilátszó rész (cm egységekben mért) magasságát \(\displaystyle x\)-szel. Így a bemerült rész magassága \(\displaystyle (40-x)\) cm, tehát a hasáb aljának távolsága a medence aljától \(\displaystyle 90-(40-x)=(50+x)\) cm, vagyis a rugó megnyúlása éppen \(\displaystyle x\) cm. A rugóállandót N/m helyett N/cm egységben is megadhatjuk: 14,4 N/cm. Ezzel megkaptuk a rugóerő nagyságát: (\(\displaystyle 14,4\) N/cm) \(\displaystyle \cdot \,x\).

A bemerült rész magassága a rugó húzóereje nélküli 24 cm-ről a rugó hatására \(\displaystyle (40-x)\) cm-re növekedett, vagyis a változás \(\displaystyle (16-x)\) cm. Ha ezt a kifejezést elosztjuk 10-zel, akkor cm helyett dm egységre váltunk. Mivel a fahasáb alapélei 8 dm, illetve 3 dm hosszúak, így minden egyes többlet dm merülés 24 liter súlyának, vagyis durván 240 N többlet felhajtóerőnek felel meg. Ez a többlet felhajtóerő tart egyensúlyt a rugóerővel:

\(\displaystyle \frac{16-x}{10}\cdot 240\,\rm{N}=(14,4\, \rm{N/cm})\, \cdot \,x\,,\)

amiből \(\displaystyle x=\) 10 cm.

\(\displaystyle b)\) Ha a fahasábot teljesen a víz felszíne fölé emeljük, akkor 30 cm-t (0,3 m-t) kell rajta emelni. Az emelés kezdetén az emelőerő nulla, a végén pedig a fahasáb 576 N-os súlya \(\displaystyle (0{,}6\,\cdot\,4\,\cdot\,24\,\cdot\,10=576\,\rm{N})\), valamint az éppen ugyanekkora rugóerő \(\displaystyle (14{,}4\,\rm{N/cm}\,\cdot \,40\,\rm{cm}=576\,\rm{N})\) összege, ami 1152 N. Az átlagos emelőerő így 576 N, tehát a kérdéses munkavégzés \(\displaystyle 576\,\rm{N}\,\cdot\,0,3\,\rm{m}=172,8\,\rm{J}\approx170\,\rm{J}\).

Megjegyzés. Energetikai megfontolásokkal is megoldhatjuk a példát. A kezdeti rugóenergia: \(\displaystyle \tfrac{1}{2}\,\cdot\,1440\,\rm{N/m}\,\cdot \,(0{,}1\,\rm{m})^2=7{,}2\,\rm{J}\), a kiemelés végén pedig \(\displaystyle \tfrac{1}{2}\,\cdot\,1440\,\rm{N/m}\,\cdot \,(0{,}4\,\rm{m})^2=115{,}2\,\rm{J}\), vagyis a növekmény 108 J. A fahasáb helyzeti energia növekménye: \(\displaystyle mgh=576\,\rm{N}\,\cdot\,0{,}3\,\rm{m}=172{,}8\,\rm{J}\), amiből még le kell vonnunk a bemerült rész helyére áramló víz helyzeti energia csökkenését: \(\displaystyle -m_\textrm{víz}gh/2=-3\,\cdot\,24\,\cdot\,10\,\cdot\,0{,}15=-108\,\rm{J}\), ami az adatok rafinált megadása miatt éppen a rugón végzett munkát ejti ki. Tehát pont annyi munkával emelhetjük ki a vízből a fahasábot, mint amennyi ahhoz kell, hogy levegőn (rugó nélkül) 30 cm magasra emeljük a hasábot.

Statisztika:

26 dolgozat érkezett.
4 pontot kapott:	Antal Áron, Bencze Mátyás, Csapó András, Hornok Máté, Jávor Botond, Kiss 668 Benedek, Nagy 639 Csenge, Sós Ádám, Sütő Áron, Szatmári Emese, Tóth Hanga Katalin, Varga Zétény.
3 pontot kapott:	Tajta Sára, Zámbó Luca.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2023. januári fizika feladatai