A G. 820. feladat (2023. május)

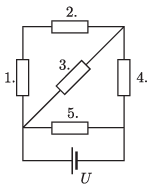
G. 820. Az ábrán látható áramkör mindegyik ellenállása \(\displaystyle 6~\mathrm{k}\Omega\)-os, a telep feszültsége \(\displaystyle U = 60\) V. Hányszor több hő fejlődik a legjobban melegedő ellenálláson, mint a legkevésbé melegedőn?

(4 pont)

A beküldési határidő 2023. június 15-én LEJÁRT.

Megoldás. A sorosan, illetve párhuzamosan kapcsolt ellenállások eredőjének képletéből, valamint az Ohm-törvényből kapjuk, hogy az egyes ellenállásokon átfolyó áramok erőssége: \(\displaystyle I_1=I_2=2\ \rm mA\), \(\displaystyle I_3=4\ \rm mA\), \(\displaystyle I_4=6\ \rm mA\) és \(\displaystyle I_5=10\ \rm mA\). A legnagyobb áram erőssége 5-szöröse a legkisebbének. Az egyforma ellenállásokon egységnyi idő alatt fejlődő hő az áramerősség négyzetével arányos, így az 5. ellenálláson 25-ször több hő fejlődik, mint az 1., vagy a 2. ellenálláson. (\(\displaystyle P_5=600\ \rm mW,\) \(\displaystyle P_1=P_2=24\ \rm mW.\))

Statisztika:

23 dolgozat érkezett.
4 pontot kapott:	Antal Áron, Bencze Mátyás, Biró Kata, Blaskovics Ádám, Földi Albert, Jávor Botond, Kiss 668 Benedek, Nagy 639 Csenge, Sós Ádám, Sütő Áron, Szabó 926 Bálint, Tajta Sára, Tóth Hanga Katalin, Žigo Boglárka.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	5 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2023. májusi fizika feladatai