 |
A G. 843. feladat (2024. február) |
G. 843. Egy \(\displaystyle 45^\circ\)-os szögben ferdén elhelyezett síktükör fölött \(\displaystyle 12~\text{cm}\) magasan egy \(\displaystyle 3~\text{cm}\) hosszú, vízszintes helyzetű világító nyilat helyezünk el. Adjuk meg, hogy mekkora és milyen helyzetű képet hoz létre a tükörtől \(\displaystyle 18~\text{cm}\)-re lévő, \(\displaystyle 20~\text{cm}\) fókusztávolságú gyűjtőlencse!
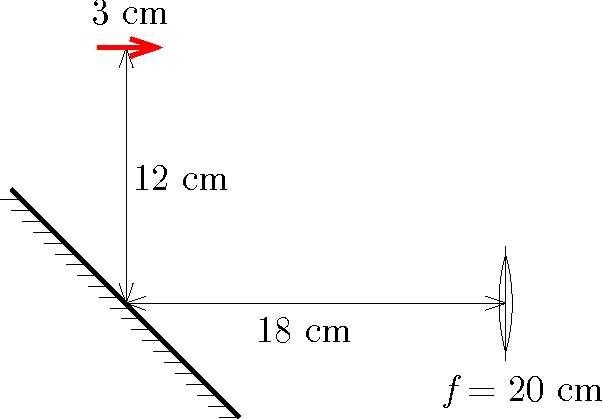
(4 pont)
A beküldési határidő 2024. március 18-án LEJÁRT.
Megoldás. A síktükör által létrehozott kép egy lefelé mutató 3 cm-es nyíl, ami 12 cm-re van a lencse optikai tengelyének és a síktükör felületének a metszéspontjától. Ennek megfelelően a helyzet annak felel meg, mintha a lencsétől 30 cm-es tárgytávolságban lévő világító nyílról készülne a kép. A leképezési törvény \(\displaystyle \left(\tfrac{1}{t}+\tfrac{1}{k}=\tfrac{1}{f}\right)\) alapján a képtávolság 60 cm, vagyis a nagyítás kétszeres, a keletkező valódi kép egy 6 cm magas, felfelé mutató nyíl.
Statisztika:
42 dolgozat érkezett. 4 pontot kapott: Barth Albert Krisztián, Blaskovics Ádám, Bús László Teodor, Csonka Áron, Fülöp Magdaléna, Görög Csanád Botond, Jávor Botond, Kis Boglárka 08, Milovecz Fruzsina Panka, Papp Emese Petra, Páternoszter Tamás, Porcsin Gréta, Sárecz Bence, Sógor-Jász Soma, Szabó Márton, Tajta Sára, Vértesi Janka, Vincze Anna. 3 pontot kapott: Chen Yu, Csáki Anikó, He Stefan, Kisida Kata, Varga 510 Csanád , Vízhányó Janka. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 6 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2024. februári fizika feladatai