A G. 851. feladat (2024. április)

G. 851. A cirkónium-dioxid törésmutatója \(\displaystyle 2{,}1\). Ebből az anyagból egy \(\displaystyle 30^\circ\)–\(\displaystyle \,60^\circ\)–\(\displaystyle \,90^\circ\)-os prizmát készítünk, amelyre az ábrán látható módon két vékony fénysugarat bocsátunk. Mekkora szöget zár be egymással a prizmából kilépő két fénysugár?

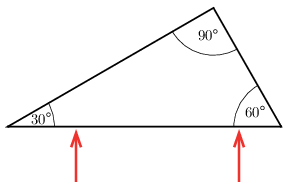
(4 pont)

A beküldési határidő 2024. május 15-én LEJÁRT.

Megoldás. A cirkónium-dioxidban a teljes visszaverődés határszöge

\(\displaystyle \alpha_\mathrm{h}=\arcsin\frac{1}{n}=28{,}4^\circ.\)

Az ábrán látható, hogy a két fénysugár – a merőleges belépés után – \(\displaystyle 30^\circ\)-os (mindenhol egyszeres fekete körívvel jelölve), illetve \(\displaystyle 60^\circ\)-os (mindenhol dupla körívvel jelölve) beesési szöggel éri el belülről a prizma határfelületét. Mindkét szög nagyobb az \(\displaystyle \alpha_\mathrm{h}\) határszögnél, így mindkét esetben teljes visszaverődést tapasztalunk. A következő határfelületet a fénysugarak – felcserélve – ugyanekkora beesési szögekkel érik el, így ismét teljes visszaverődés történik. Végül harmadszorra mindkét fénysugár merőlegesen kilép a prizmából.

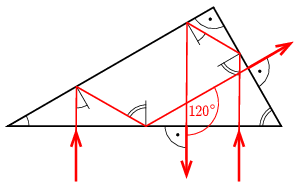
Az ábráról leolvasható, hogy a két kilépő fénysugár iránya \(\displaystyle 120^\circ\)-os szöget zár be egymással (piros körívvel jelölve).

Megjegyzés. A merőleges be- és kilépéskor a fény egy kis része visszaverődik (részleges visszaverődés). A kilépésnél visszaverődő fénysugarak bejárják a fényutat visszafelé, és így az eredeti belépő fénysugarak helyén, azokkal ellentétes irányba lépnek ki. Ezek a fénysugarak így egymással párhuzamosak lesznek.
Ezek intenzitása azonban jóval kisebb. A feladat teljes értékű megoldásához nem várjuk el ezek vizsgálatát.

Statisztika:

41 dolgozat érkezett.
4 pontot kapott:	Barth Albert Krisztián, Blaskovics Ádám, Blaskovics Bálint, Bohner Emese, Csáki Anikó, Fülöp Magdaléna, Görög Csanád Botond, He Stefan, Hollósi Dominik, Jávor Botond, Kis Boglárka 08, Szabó András, Szabó Márton, Vértesi Janka, Vincze Anna.
3 pontot kapott:	Bús László Teodor, Chen Yu, Csonka Áron, Horváth 001 Botond , Kisida Kata, Méhes Mátyás , Papp Emese Petra, Porcsin Gréta, Tajta Sára, Vízhányó Janka.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2024. áprilisi fizika feladatai