A G. 853. feladat (2024. május)

G. 853. Egy rendőrautó az autópályán halad. Sebességét a számítógépes rendszer rögzítette, ez alapján készült az alábbi $\displaystyle v_\mathrm{r}(t)$ grafikon. Egy motoros egyszer csak megelőzi a rendőrautót, a rendőrautó méri a motoros sebességét. Az $\displaystyle u_\mathrm{m}(t)$ grafikon azt mutatja, hogy mekkora a motoros sebessége a rendőrautóhoz viszonyítva.

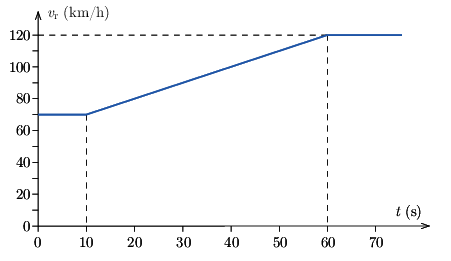
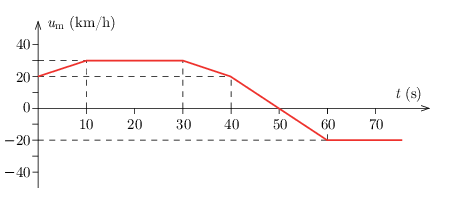
$\displaystyle a)$ Rajzoljuk meg a motoros földhöz viszonyított sebességének $\displaystyle v_\mathrm{m}(t)$ grafikonját!

$\displaystyle b)$ A grafikonokon ábrázolt időtartam alatt mikor volt a legtávolabb egymástól a két jármű? Mekkora ez a távolság?

$\displaystyle c)$ A 60. másodperc után állandó sebességgel haladnak tovább. Mikor előzi vissza a rendőrautó a motorost?

Közli: Baranyai Klára, Veresegyház

(4 pont)

A beküldési határidő 2024. június 17-én LEJÁRT.

Megoldás. $\displaystyle a)$ A motoros földhöz viszonyított sebessége:

$\displaystyle v_\mathrm{m}(t)=v_\mathrm{r}(t)+u_\mathrm{m}(t),$

ami alapján megszerkeszthetjük a grafikont (felső grafikon piros görbéje):

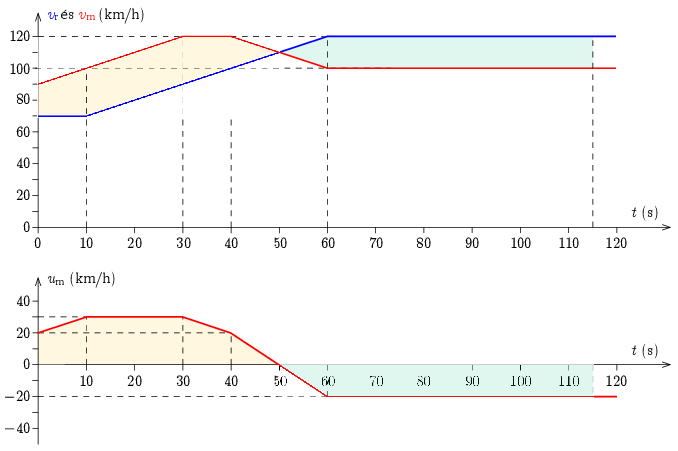
$\displaystyle b)$ Egy rövid $\displaystyle \Delta t$ idő alatt a két jármű közötti távolság változása:

$\displaystyle \Delta s=\left[v_\mathrm{m}(t)-v_\mathrm{r}(t)\right]\Delta t=u_\mathrm{m}(t)\Delta t,$

tehát egy adott idő alatt a távolság változását a két sebesség grafikon közötti terület, vagy (egyszerűbben) a relatív sebesség grafikon alatti terület adja meg. A $\displaystyle t=0$ pillanatban előzi le a motoros a rendőrautót, a távolságuk ekkor nulla. A távolság addig növekszik, amíg a motoros sebessége a nagyobb ($\displaystyle t=50\,\mathrm{s}$). A legnagyobb távolság a rajzon halványpirossal jelölt terület nagysága:

$\displaystyle s_\mathrm{max}=10\cdot25+20\cdot30+10\cdot25+10\cdot10=1200\,\mathrm{s\cdot\frac{km}{h}}=\frac{1}{3}\,\mathrm{km}.$

$\displaystyle c)$ Ezután a rendőrautó a gyorsabb. Akkor éri utol a motorost, amikor a távolságuk újra nulla lesz. Azt kell megkeresnünk, hogy mikor lesz a rajzon halványkékkel jelölt terület egyenlő $\displaystyle s_\mathrm{max}$-szal:

$\displaystyle 10\cdot10+(t_0-60)\cdot20=1200,$

amiből $\displaystyle t_0=115\,\mathrm{s}.$

Statisztika:

39 dolgozat érkezett.
4 pontot kapott:	Barth Albert Krisztián, Blaskovics Ádám, Blaskovics Bálint, Bohner Emese, Fülöp Magdaléna, Gerlei Dániel, Havas Dániel, Horváth 001 Botond , Kis Boglárka 08, Németh Ábel, Porcsin Gréta, Sógor-Jász Soma, Szabó András, Szabó Márton, Tajta Sára, Varga 511 Vivien.
3 pontot kapott:	Bús László Teodor, Horváth Kristóf Dominik, Jávor Botond, Kisida Kata, Sipos Dániel Sándor, Vincze Anna.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2024. májusi fizika feladatai