A G. 855. feladat (2024. május)

G. 855. Newton nem a szokásos alakjában $\displaystyle \left(\tfrac{1}{t}+\tfrac{1}{k}=\tfrac{1}{f}\right)$ írta fel a leképezési törvényt. Ő a tárgyoldali fókuszponttól mérte az $\displaystyle x_\mathrm{t}$ fókuszontúli tárgytávolságot, illetve a képoldali fókuszponttól mérte az $\displaystyle x_\mathrm{k}$ fókuszontúli képtávolságot, ahogy ez az ábrán látható.

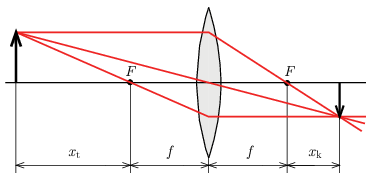
$\displaystyle a)$ Adjuk meg a legegyszerűbb alakban a leképezési törvényt ezekkel a paraméterekkel!

$\displaystyle b)$ Hogyan alkalmazható ez a képlet szórólencsékre?

(4 pont)

A beküldési határidő 2024. június 17-én LEJÁRT.

Megoldás. $\displaystyle a)$ A kitűzésben szereplő ábráról látható, hogy

amiket beírva a leképzési törvény szokásos alakjába:

$\displaystyle \frac{1}{x_\mathrm{t}+f}+\frac{1}{x_\mathrm{k}+f}=\frac{1}{f}.$

Az egyenletet mindhárom nevezővel beszorozva és rendezve:

$\displaystyle x_\mathrm{t}x_\mathrm{k}=f^2.$

$\displaystyle b)$ A szórólencse fókusztávolsága negatív, de a képletben $\displaystyle f^2$ szerepel, így ez nem okozna különbséget. Vegyük úgy figyelembe a fókusztávolság előjelét, hogy a távolságokat a túloldali fókusztól mérjük!

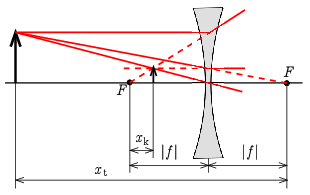
Az ábra alapján:

amiket beírva a leképzési törvény szokásos alakjába:

$\displaystyle \frac{1}{x_\mathrm{t}-|f|}+\frac{1}{x_\mathrm{k}-|f|}=-\frac{1}{|f|}.$

Az egyenletet mindhárom nevezővel beszorozva és rendezve:

$\displaystyle x_\mathrm{t}x_\mathrm{k}=f^2,$

a gyűjtőlencsével megegyezően.

Statisztika:

28 dolgozat érkezett.
4 pontot kapott:	Fülöp Magdaléna, Porcsin Gréta, Szabó András.
3 pontot kapott:	Barth Albert Krisztián, Blaskovics Ádám, Bora Ádám, Dömők Bernadett, Hollósi Dominik, Jávor Botond, Szabó Márton.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. májusi fizika feladatai