 |
A G. 861. feladat (2024. október) |
G. 861. Panni sétálni vitte Fickó nevű kutyáját. A sugárúton Panni \(\displaystyle 0{,}8~\mathrm{m}/\mathrm{s}\) sebességgel haladt, amikor egy hársfa mellett elejtette a lakáskulcsát. Fickó ekkor a hársfától 4 méterre lévő szemeteskukánál járt. Fickó sebessége \(\displaystyle 1{,}2~\mathrm{m}/\mathrm{s}\) volt. Amikor Fickó a kukától \(\displaystyle 3{,}6\) méterre lévő lámpaoszlophoz ért, visszafordult, és a kuka és a lámpaoszlop között ide-oda szaladt \(\displaystyle 1{,}2~\mathrm{m}/\mathrm{s}\) sebességgel. Amikor Panni a kukához ért, észrevette, hogy elejtette a kulcsot, ezért visszafordult érte. Ő végig \(\displaystyle 0{,}8~\mathrm{m}/\mathrm{s}\) sebességgel mozgott.
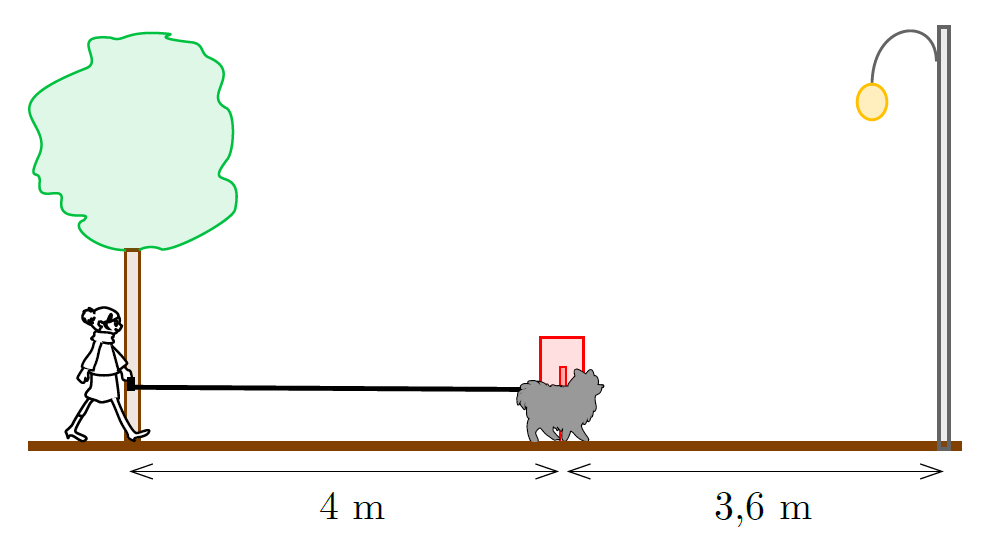
Hogyan változott a végig feszes póráz hossza a kulcs elejtésétől annak kézhez vételéig? Készítsünk grafikont!
Közli: Baranyai Klára, Veresegyház
(4 pont)
A beküldési határidő 2024. november 15-én LEJÁRT.
Megoldás. Az 1. ábrán Panni (piros vonal) és Fickó (kék vonal) elmozdulás-idő grafikonját ábrázoltuk. Az \(\displaystyle x\) tengely origója a hársfánál van, az időt pedig attól kezdve mérjük, hogy Panni elhalad a fa mellett. Panni \(\displaystyle 5\,\mathrm{s}\) alatt teszi meg a fa és a szemeteskuka közötti távolságot, Fickó pedig \(\displaystyle 3\,\mathrm{s}\) alatt ér a szemeteskukától a lámpáig.
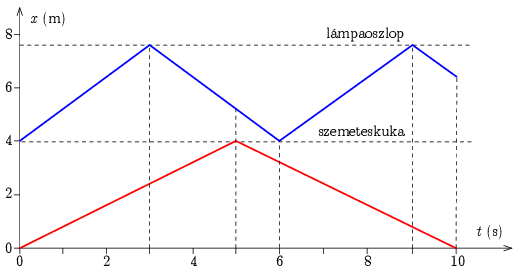
1. ábra
A póráz hossza minden pillanatban a két helyzet különbsége. Amikor mindketten egyenletes sebességgel mozognak, akkor a kötél hossza is egyenletesen változik, így csak azokban a pontokban kell számolnunk, ahol valamelyik grafikonnak töréspontja van. Ezekben az időpontokban Fickó és Panni helyzetét, valamint a póráz \(\displaystyle d\) hosszát az alábbi táblázatban foglaltuk össze.
A táblázat alapján már könnyen megrajzolhatjuk a 2. ábrát, melyen a póráz hossza látható az idő függvényében.
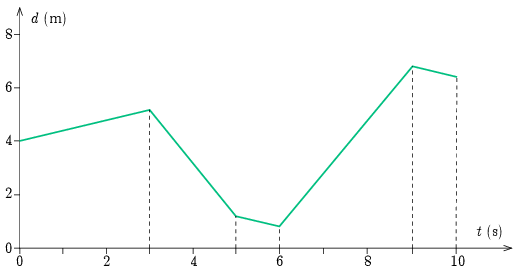
2. ábra
Statisztika:
49 dolgozat érkezett. 4 pontot kapott: Békési Máté, Blaskovics Bálint, Dombóvári Nándor, Hegedüs Márk, Horváth Zsombor, Huba Zsombor , Kakas Noel, Kámán-Gausz Péter, Kis Dániel, Klenkó Éva Borbála, Kossár Benedek Balázs, Kovács Artúr-Lehel, Kovács Tamás , Medgyesi András, Németh Ábel, Palik Csenge, Patócs 420 Péter, Sipos Dániel Sándor, Szabó András, Szighardt Anna, Szűcs Kitti, Tóth Domonkos, Zsuga Medárd. 3 pontot kapott: Csonka Áron, Lakatos Levente, Majer Veronika, Sógor-Jász Soma, Vincze Blanka Anna, Vízhányó Janka. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 5 dolgozat.
A KöMaL 2024. októberi fizika feladatai