 |
A G. 864. feladat (2024. október) |
G. 864. Az ábrán látható kapcsolási rajz szerint összeállított, \(\displaystyle U=24~\mathrm{V}\) egyenfeszültséget szolgáltató feszültségforrásról táplált áramkörben a voltmérőről \(\displaystyle 10~\mathrm{V}\), az \(\displaystyle \mathrm{A}_1\) ampermérőről \(\displaystyle 0{,}2~\mathrm{A}\), az \(\displaystyle \mathrm{A}_2\) ampermérőről pedig \(\displaystyle 0{,}7~\mathrm{A}\) olvasható le.
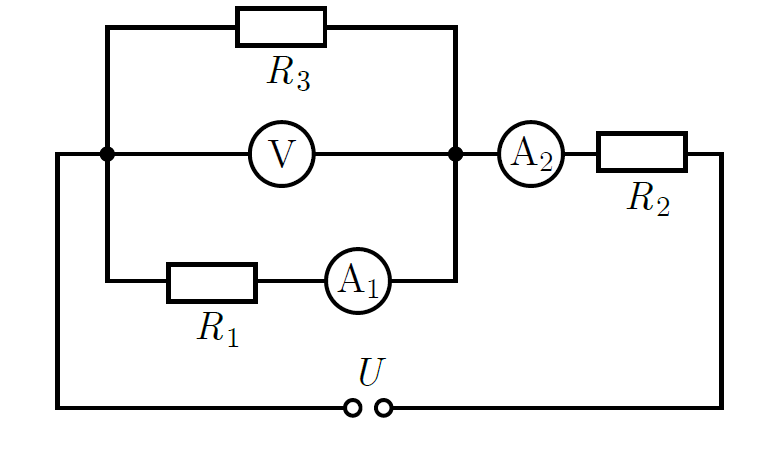
\(\displaystyle a)\) Határozzuk meg az egyes ellenállások értékét!
\(\displaystyle b)\) Mennyi hő fejlődik 2 perc alatt az áramkörben?
Mindhárom mérőműszer ideálisnak tekinthető. A feszültségforrás belső ellenállása és az összekötő vezetékek ellenállása elhanyagolható.
Tornyai Sándor Fizikaverseny, Hódmezővásárhely
(4 pont)
A beküldési határidő 2024. november 15-én LEJÁRT.
Megoldás. a) Az \(\displaystyle R_1\) és \(\displaystyle R_3\) ellenállásokon a voltmérő által mutatott feszültség, \(\displaystyle U_{1,3}=10\,\mathrm{V}\) esik, így az \(\displaystyle R_2\) ellenállásra \(\displaystyle U_2=U-U_{1,3}=14\,\mathrm{V}\) jut. Az \(\displaystyle R_1\) és \(\displaystyle R_2\) ellenállások áramát közvetlenül mérik a velük sorba kapcsolt árammérők: \(\displaystyle I_1=0{,}2\,\mathrm{A}\) és \(\displaystyle I_2=0{,}7\,\mathrm{A}\). Az \(\displaystyle R_3\) ellenállás árama a két áram különbsége: \(\displaystyle I_3=I_2-I_1=0{,}5\,\mathrm{A}\).
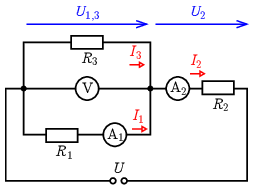
Az egyes ellenállások nagysága az Ohm-törvény alapján:
\(\displaystyle R_1=\frac{U_1}{I_1}=50\,\Omega,\qquad R_2=\frac{U_2}{I_2}=20\,\Omega,\qquad\textrm{és}\qquad R_3=\frac{U_3}{I_3}=20\,\Omega.\)
b) Az áramkör teljesítménye a kapocsfeszültség és a főágbeli áram szorzata:
\(\displaystyle P=UI_2=24\,\mathrm{V}\cdot 0{,}7\,\mathrm{A}=16{,}8\,\mathrm{W}.\)
Megjegyzés. A teljesítmény kiszámítható az egyes ellenállások teljesítményének összegeként is a \(\displaystyle P_i=U_iI_i\), a \(\displaystyle P_i=R_iI_i^2\) és a \(\displaystyle P_i=U_i^2/R_i\) összefüggések valamelyikének használatával:
\(\displaystyle P=U_1I_1+U_2I_2+U_3I_3=I_1^2R_1+I_2^2R_2+I_3^ˇR_3=\frac{U_1^2}{R_1}+\frac{U_2^2}{R_2}+\frac{U_3^2}{R_3}=16{,}8\,\mathrm{W}.\)
Az áramkörben 2 perc alatt fejlődő hő:
\(\displaystyle Q=Pt=16{,}8\,\mathrm{W}\cdot 120\,\mathrm{s}=2016\,\mathrm{J}\approx 2\,\mathrm{kJ}.\)
Megjegyzés. A ma használt digitális voltmérők belső ellenállása legalább \(\displaystyle 1\,\mathrm{M}\Omega\), így a feladatban előforduló ellenállásokhoz képest nagyon nagy, ,,végtelennek'' tekinthető, tehát az ideális műszer közelítés mindenképp jogos. Az ampermérők belső ellenállása viszont a méréshatártól függően akár \(\displaystyle 1\,\mathrm{k}\Omega\) is lehet, ami egyáltalán nem elhanyagolható az ellenállások értéke mellett. (Épp ezért célszerű úgy kialakítani a mérő áramkört, hogy a voltmérő csak az ellenálláson eső feszültséget mérje, az ampermérőn esőt ne.) Esetünkben az lehet a megoldás, hogy az ampermérőt \(\displaystyle 10\,\mathrm{A}\)-es méréshatáron használjuk, ahol az ellenállása csak néhány tized ohm, ami ha nem is nulla, de aránylag kicsi az ellenállások értéke mellett. (Ennek azonban az az ára, hogy az áram értékét kevésbé pontosan tudjuk mérni.)
Statisztika:
A G. 864. feladat értékelése még nem fejeződött be.
A KöMaL 2024. októberi fizika feladatai