A G. 866. feladat (2024. november)

G. 866. Egy kétszeresen meghajlított vékony cső három, elegendően hosszú részből áll. A középső rész vízszintes, az első rész \(\displaystyle 30^\circ\)-os szöget, a harmadik rész pedig \(\displaystyle 45^\circ\)-os szöget zár be a vízszintessel. A szakaszok ugyanabban a függőleges síkban fekszenek, az egyes szakaszokat rövid, törésmentes hajlatok kötik össze. A cső bal oldali végén egy csap annyi levegőt zár el a külvilágtól, hogy a bal oldali csőszakasz alján \(\displaystyle L\) hosszúságú higanyszál legyen nyugalmi állapotban. A csapot hirtelen kinyitjuk, emiatt a higanyszál súrlódásmentesnek tekinthető mozgásba kezd. Induláskor a higanyszál eleje a cső első és második szakaszának találkozásánál van.

A higanyszálnak maximálisan mekkora része kerül be a cső harmadik szakaszába?

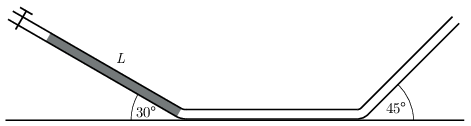
Közli: Baranyai Klára, Veresegyház

(4 pont)

A beküldési határidő 2024. december 16-án LEJÁRT.

Megoldás. A higany nem juthat be teljesen a meredekebb csőszakaszba, mert akkor a higany súlypontja magasabbra kerülne a kiindulási helyzetnél. A higanyszál helyzeti energiája a vízszintes szakaszhoz viszonyítva a kezdeti helyzetben \(\displaystyle \tfrac{mgL}{4}\), ahol kihasználtuk, hogy a félszabályos háromszög kisebbik befogója fele az átfogónak, valamint a higanyszál tömegközéppontja a felénél van. A túloldali szélső helyzetben (a veszteségmentesség miatt) ugyanekkora lesz a higanyszál magassági energiája. Jelöljük \(\displaystyle x\)-szel a higanyszál azon részének a hosszúságát, ami bejut a \(\displaystyle 45^\circ\)-os csőszakaszba. Ennek a résznek a tömege \(\displaystyle \tfrac{x}{L}m\), tehát a helyzeti energiája: \(\displaystyle \tfrac{x}{L}mg\tfrac{x}{2\sqrt{2}}.\) A két állapot helyzeti energiáját egyenlővé téve megkapjuk a kérdéses értéket:

\(\displaystyle x=\frac{L}{\sqrt[4]{2}}\approx 0{,}84\,L.\)

Statisztika:

A G. 866. feladat értékelése még nem fejeződött be.

A KöMaL 2024. novemberi fizika feladatai