A G. 867. feladat (2024. november)

G. 867. Egy kaloriméterben jég és víz keveréke van. A kalorimétert állandó fűtőteljesítménnyel melegítjük, és mérjük a tartalmának hőmérsékletét, amelyet az idő függvényében ábrázoltunk.

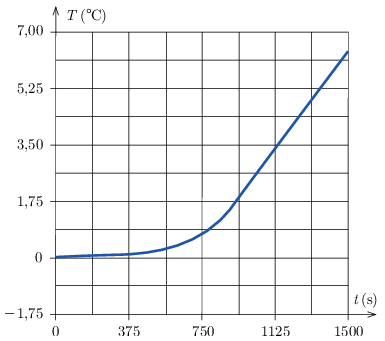
A mérés végén $\displaystyle 850~\mathrm{ml}$ víz volt a kaloriméterben. Állapítsuk meg, hogy mekkora a fűtőteljesítmény, valamint azt, hogy mennyi jég volt kezdetben a kaloriméterben!

(4 pont)

A beküldési határidő 2024. december 16-án LEJÁRT.

Megoldás. A kaloriméterben a jég megolvad, majd a víz felmelegszik. Interpoláció segítségével ezt a két folyamatot a hőmérséklet - idő grafikonon két egyenes szakaszra bonthatjuk, ahogy ezt az ábra mutatja.

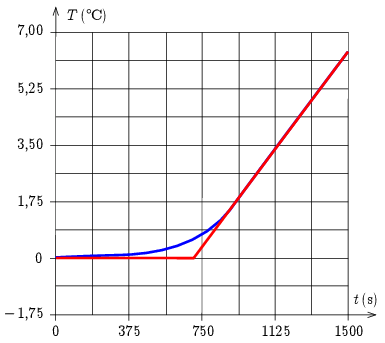
Ez a módszer egy közelítés, hiszen amikor már csak nagyon kevés jég van a kaloriméterben, akkor a víz felmelegedése már elindul. Ugyancsak közelítés az is, hogy a most következő számítások során a kaloriméter hőkapacitását elhanyagoljuk.

A vízszintes szakasz azt mutatja, hogy nagyjából $\displaystyle t_1=700\,\mathrm{s}$-ig tart a jég olvadása, majd körülbelül $\displaystyle t_2=800\,\mathrm{s}$ alatt $\displaystyle 0\,^{\circ}\mathrm{C}$-ról hozzávetőlegesen $\displaystyle 6{,}4\,^{\circ}\mathrm{C}$-ra melegszik a kaloriméterben lévő $\displaystyle 850\,\mathrm{ml}$ víz. A víz közismert fajhője ($\displaystyle c=4{,}2\,\mathrm{\tfrac{J}{g^{\circ}C}}$) alapján kiszámíthatjuk, hogy $\displaystyle 850\,\mathrm{g}$ víz $\displaystyle 6{,}4\,^{\circ}\mathrm{C}$-kal történő felmelegítéséhez $\displaystyle Q_2=cm\Delta T=22800\,\mathrm{J}$ hő szükséges, tehát a kaloriméter fűtőteljesítménye: $\displaystyle P=\tfrac{Q_2}{t_2}=28{,}5\,\mathrm{W}$.

A felfűtés első szakaszában 700 s alatt a kaloriméter fűtőszála $\displaystyle Q_1=Pt_1=19900\,\mathrm{J}$ hőt adott le, ami $\displaystyle \Delta m=\tfrac{Q_1}{L_{\mathrm{olv}}}=60\,\mathrm{g}$ jég megolvasztásához elegendő. (A jég olvadáshője: $\displaystyle L_{\mathrm{olv}}=334\,\mathrm{\tfrac{J}{g}}$.) Tehát kezdetben 60 gramm jég és 790 ml víz volt a kaloriméterben.

Statisztika:

37 dolgozat érkezett.
4 pontot kapott:	Békési Máté, Csáki Anikó, Csonka Áron, Gerőcs-Tóth Dániel , Hegedüs Márk, Huba Zsombor , Kovács Artúr-Lehel, Majer Veronika, Németh Ábel, Sipeki Andor, Szabó András, Szilaj Petra, Tóth Domonkos, Vízhányó Janka.
3 pontot kapott:	Bodó Rókus Dániel, Horváth Zsombor, József Áron, Lakatos Levente, Molnár Sámuel , Patócs 420 Péter, Sógor-Jász Soma, Szighardt Anna.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. novemberi fizika feladatai