A G. 869. feladat (2024. december)

G. 869. Egy gépkocsi első, illetve hátsó kerekei egy olyan téglalap csúcsaiban helyezkednek el, melynek oldalai 4 m és 2 m, ahogy ez az ábrán látható.

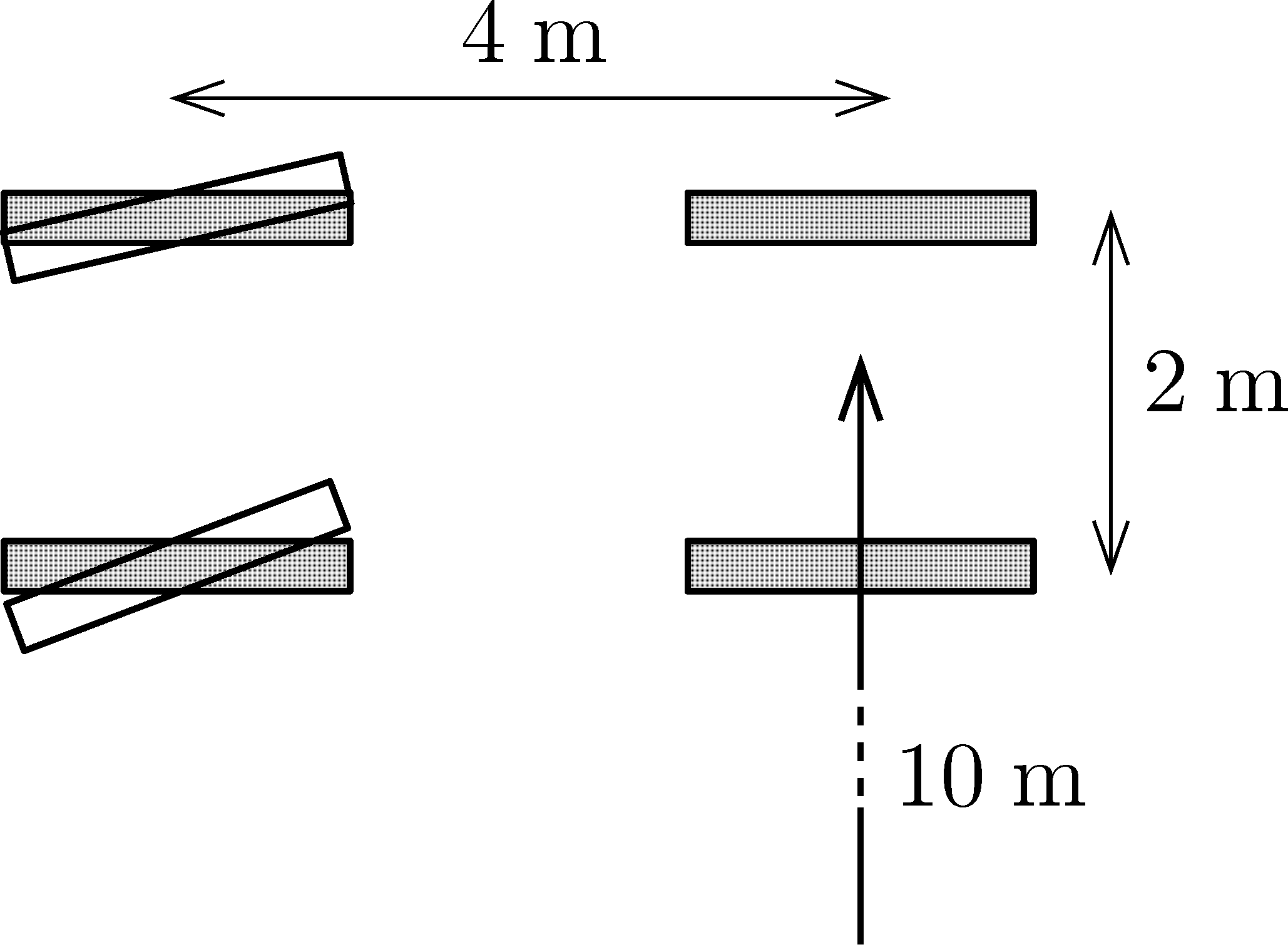
a) Ha a hátsó kerekek alkotta szakasz középpontja az autó kanyarodásakor $\displaystyle {R=10}~\mathrm{m}$ sugarú körön fordul körbe, akkor az autó vizes kerekei mekkora sugarú köröket rajzolnak a száraz aszfaltra?

b) Kanyarodás közben mekkora az első kerekek függőleges tengely körüli szögelfordulása?

(3 pont)

A beküldési határidő 2025. január 15-én LEJÁRT.

Megoldás. a) Az autó bal hátsó kereke 9 m, a jobb hátsó kerék pedig 11 m sugarú körön fordul. Az autó tiszta rotációt végez, ezért minden pontja olyan körön mozog, aminek ugyanott van a középpontja. Pitagorasz-tétel segítségével számíthatjuk ki, hogy a bal első kerék $\displaystyle r_1=\sqrt{9^2+4^2}\,\mathrm{m}=9{,}85\,\mathrm{m}$, míg a jobb első kerék $\displaystyle r_2=\sqrt{11^2+4^2}\,\mathrm{m}=11{,}7\,\mathrm{m}$ sugarú körön mozog.

b) A kerekeknek úgy kell elfordulniuk, hogy síkjuk merőleges legyen a körpályájuk sugarára. Merőlegesszárú szögek alapján számíthatjuk ki a két első kerék elfordulását:

$\displaystyle \alpha_1=\arcsin\frac{4}{9{,}85}=\arctan\frac{4}{9}=24^\circ,$

illetve

$\displaystyle \alpha_2=\arcsin\frac{4}{11{,}7}=\arctan\frac{4}{11}=20^\circ.$

Megállapíthatjuk, hogy a két első kerék elfordulási szöge nem azonos (esetünkben a két szögelfordulás közti különbség $\displaystyle 4^\circ$), a külső körön futó kerék elfordulása a kisebb.

Megjegyzések. 1. A feladatot megoldhatjuk geometriai szerkesztéssel (körzővel, vonalzóval), majd a kérdéses sugarakat és szögeket lemérhetjük vonalzóval és szögmérővel. Ez a módszer is teljes értékű megoldásként fogadható el.

2. A valóságban a jobb útfekvés érdekében a kormányozott kerekeket nemcsak elforgatják, hanem meg is döntik.

Statisztika:

24 dolgozat érkezett.
3 pontot kapott:	Békési Máté, Csáki Anikó, Hegedüs Márk, Kovács Artúr-Lehel, Kovács Tamás , Majer Veronika, Medgyesi András, Molnár Sámuel , Szighardt Anna, Szilaj Petra, Vízhányó Janka.
2 pontot kapott:	Hollósi Dominik, Horváth Zsombor, Huba Zsombor .
1 pontot kapott:	5 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. decemberi fizika feladatai