A G. 878. feladat (2025. február)

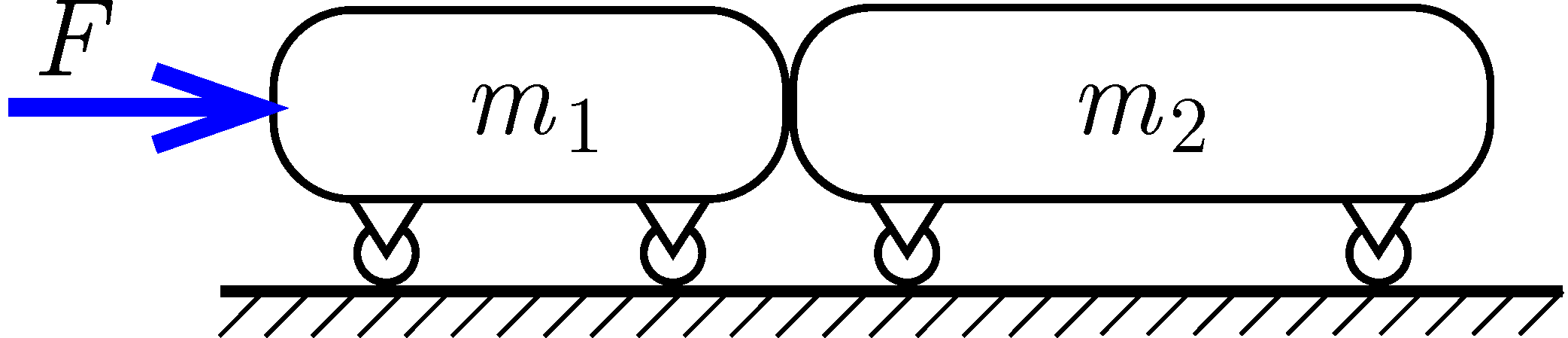
G. 878. Vízszintes sínen, szorosan egymás mellett áll két kiskocsi. Az egyik $\displaystyle 100~\mathrm{g}$, a másik $\displaystyle 150~\mathrm{g}$ tömegű. A kocsik a sínen súrlódás nélkül mozoghatnak. A kisebb tömegű kocsival megtoljuk a nagyobbat úgy, hogy a kisebbikre $\displaystyle 0{,}5~\mathrm{N}$ erőt fejtünk ki vízszintes irányban, az ábra szerint.

a) Mekkora a kiskocsik közös gyorsulása?

b) Mekkora nyomóerő lép fel a kocsik között?

c) Módosul-e az előző két kérdésre adott válasz, ha a nagyobb kocsira fejtünk ki a másik felé irányuló, ugyancsak $\displaystyle 0{,}5~\mathrm{N}$ nagyságú, vízszintes irányú erőt?

(4 pont)

A beküldési határidő 2025. március 17-én LEJÁRT.

Megoldás. Vegyük fel az adatokat (a tömegeket váltsuk kg-ra), és tüntessük fel a kiszámolandó mennyiségeket: $\displaystyle m_1=100\,\mathrm{g}=0{,}1\,\mathrm{kg}$, $\displaystyle m_2=150\,\mathrm{g}=0{,}15\,\mathrm{kg}$, $\displaystyle F=0{,}5\,\mathrm{N}$. $\displaystyle a=?$ $\displaystyle F_\mathrm{ny}=?$

a) Mivel a két kocsi együtt mozog, úgy tekinthetjük, mintha egyetlen $\displaystyle (m_1+m_2)$ tömegű kocsi mozogna, amelynek gyorsulása:

$\displaystyle a=\frac{F}{m_1+m_2}=\frac{0{,}5\,\mathrm{N}}{0{,}25\,\mathrm{kg}}=2\,\mathrm{\frac{m}{s^2}}.$

b) Egyszerűbb a nagyobb tömegű kocsit vizsgálnunk, mert arra vízszintesen csak a kisebb kocsi hat, mégpedig a kérdéses nyomóerővel:

$\displaystyle F_\mathrm{ny}=m_2a=0{,}15\,\mathrm{kg}\cdot 2\,\mathrm{\frac{m}{s^2}}=0{,}3\,\mathrm{N}.$

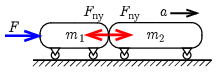
Megjegyzés. Természetesen tekinthetjük a kisebb tömegű kocsira ható nyomóerőt is, ami az ábrán látható módon éppen az előbb kiszámított nyomóerő ellenereje $\displaystyle (-F_\mathrm{ny})$. A kisebb tömegű kocsira felírható mozgásegyenlet:

$\displaystyle F–F_\mathrm{ny}=m_1a,$

amiből

$\displaystyle F_\mathrm{ny}=F-m_1a=0{,}5\,\mathrm{N}-0{,}1\,\mathrm{kg}\cdot 2\,\mathrm{\tfrac{m}{s^2}}=0{,}3\,\mathrm{N}.$

c) A két kiskocsi együttes gyorsulása nem függhet attól, hogy melyik irányból hat rájuk a külső $\displaystyle F$ erő, tehát a gyorsulásra a megoldás megegyezik az a) válasszal: $\displaystyle 2\,\mathrm{\tfrac{m}{s^2}}$.

A két kiskocsi közötti nyomóerő viszont függ attól, hogy melyik oldalon hat az $\displaystyle F$ erő. Ha a jobb oldalon hat $\displaystyle 0{,}5\,\mathrm{N}$ erő, akkor most a bal oldali kocsira könnyebb elvégezni a számolást:

$\displaystyle F'_\mathrm{ny}=m_1a=0{,}1\,\mathrm{kg}\cdot 2\,\mathrm{\frac{m}{s^2}}=0{,}2\,\mathrm{N}.$

Megjegyzés. Ilyenkor a jobb oldali kocsira eredőben $\displaystyle 0{,}5\,\mathrm{N}–0{,}2\,\mathrm{N}=0{,}3\,\mathrm{N}$ erő hat, ami a $\displaystyle 0{,}15\,\mathrm{kg}$ tömegű kocsit az elvárt $\displaystyle 2\,\mathrm{\tfrac{m}{s^2}}$ gyorsulással mozgatja.

Statisztika:

41 dolgozat érkezett.
4 pontot kapott:	Békési Máté, Blaskovics Bálint, Csáki Anikó, Csonka Áron, Dombóvári Nándor, Hegedüs Márk, Hollósi Dominik, Horváth Zsombor, József Áron, Kakas Noel, Kámán-Gausz Péter, Kiss Lukács Dániel, Kossár Benedek Balázs, Kovács Tamás , Lakatos Levente, Macskássy Márk, Majer Veronika, Márkus János Teodor , Medgyesi András, Nemes Máté Imre, Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sipos Dániel Sándor, Sógor-Jász Soma, Szabó Milos Farkas, Szighardt Anna, Szilaj Petra, Szűcs Kitti, Tóth Domonkos.
3 pontot kapott:	Molnár Sámuel , Sipeki Andor, Szabó András, Vízhányó Janka.
1 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. februári fizika feladatai