 |
A G. 881. feladat (2025. március) |
G. 881. Egy hosszú futószalag 2 m széles és 0,5 m/s nagyságú, állandó sebességgel mozog. Egy távirányításos játékautó úgy jut el a futószalag egyik szélétől a másikig, hogy a futószalaghoz képest nyugalmi helyzetből indul, a futószalaghoz képest mindig a szalagra merőleges irányban mozog, egyenletesen gyorsul a futószalag közepéig, ahol a szalaghoz képest 1 m/s sebességet ér el, majd ugyanolyan módon egyenletesen lassul, és végül a szalaghoz képest nullára csökken a sebessége.
a) A futószalag mennyivel viszi előbbre a kisautót az átkelése közben?
b) Rajzoljuk meg vázlatosan a kisautó pályáját a talajhoz képest!
(4 pont)
A beküldési határidő 2025. április 15-én LEJÁRT.
Megoldás. a) A szalagra merőlegesen a kisautó átlagsebessége 0,5 m/s, tehát a 2 m széles szalagon 4 s alatt ér át. Mivel a szalag sebessége mindenhol éppen a kisautó szalagra merőleges sebességösszetevőjének átlagával egyezik meg, így ennyi idő alatt a szalag éppen a saját szélességével, vagyis 2 m-rel mozgatja előbbre.
b) A kisautó pályája két parabolaívből áll, melyek egy 2 × 2 m-es négyzetben helyezkednek el. A pálya a négyzet egyik sarkából, a szalag szélével párhuzamosan indul, és az innen induló átló másik végében végződik, ugyancsak a szalag szélével párhuzamosan. A pálya a négyzet közepére középpontosan szimmetrikus.
Bár a gyakorlat b) pontja csak vázlatos rajzot kér, mégis tanulságos a pálya egyenletének felírása:
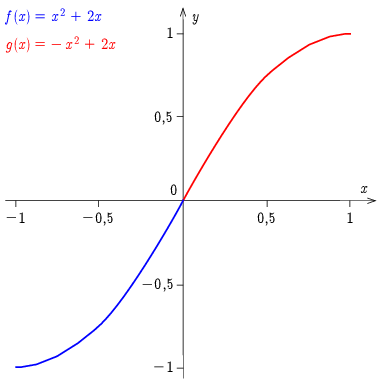
y=2x±x2,
ahol az origó a négyzet középpontjában van, továbbá x-et és y-t méterben értjük. Az értelmezési tartomány: −1≤x≤1, és az értékkészlet ugyanilyen intervallum: −1≤y≤1. Negatív x-ek esetén az egyenletben a pozitív előjel érvényes, pozitív x-ekre pedig a negatív előjel. A pálya rajza az ábrán látható.
Statisztika:
41 dolgozat érkezett. 4 pontot kapott: Békési Máté, Csáki Anikó, Csonka Áron, Dombóvári Nándor, Hegedüs Márk, Horváth Zsombor, Kossár Benedek Balázs, Kovács Artúr-Lehel, Lakatos Levente, Macskássy Márk, Majer Veronika, Medgyesi András, Molnár Sámuel , Patócs 420 Péter, Rácz Koppány Bendeguz, Sipos Dániel Sándor, Sógor-Jász Soma, Szabó András, Szighardt Anna, Vincze Blanka Anna, Vízhányó Janka. 3 pontot kapott: Kovács Tamás , Németh Ábel, Sándor Ákos, Sipeki Andor, Tóth Domonkos. 2 pontot kapott: 10 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2025. márciusi fizika feladatai
|
|

