 |
A G. 882. feladat (2025. március) |
G. 882. Az ábrán látható rendszer egyensúlyban van, a középső kötél vízszintes helyzetű.
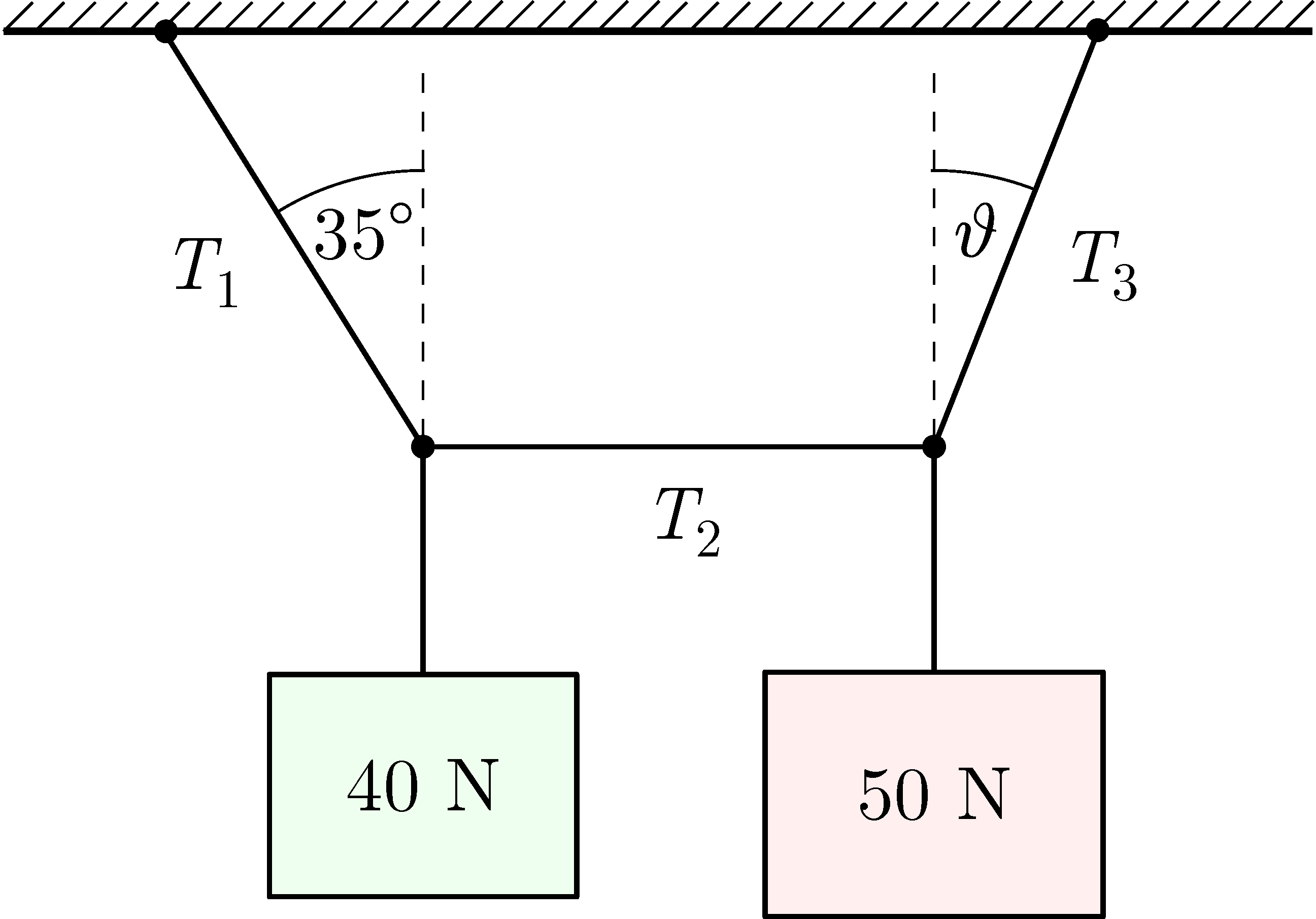
a) Milliméterpapíron, vonalzóval és szögmérővel történő szerkesztéssel határozzuk meg a kötélszárakban ható három erőt, valamint az ismeretlen \(\displaystyle \vartheta\) szöget!
b) Becsüljük meg, hogy a szerkesztés segítségével a kérdéses adatokat hány százalékos hibával kaptuk meg!
(4 pont)
A beküldési határidő 2025. április 15-én LEJÁRT.
Megoldás. a) A kényelem kedvéért a milliméterpapíron a skálát úgy válasszuk meg, hogy 1 N erő 1 mm-t jelentsen. A szerkesztést az alábbi ábra mutatja:
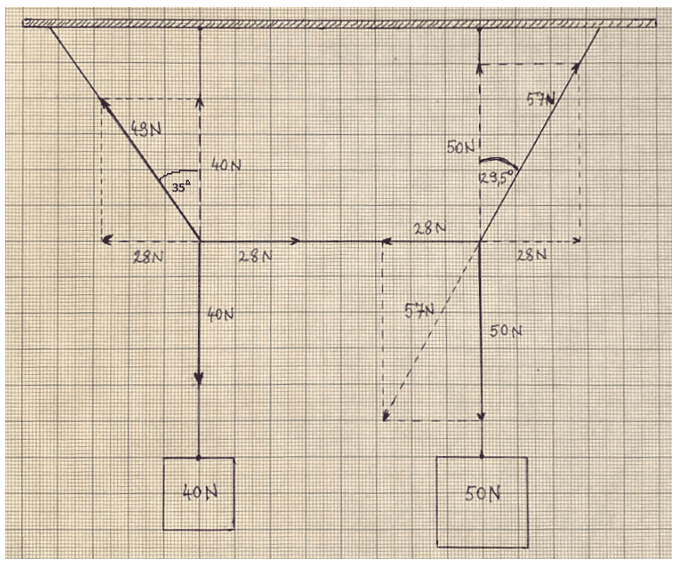
A tartóköteleknek két csomópontja van, azokba három-három kötélszár fut be, az ezekhez tartozó kötélerők az egyes csomópontokban kiegyensúlyozzák egymást. A szerkesztést a bal oldali csomóponttal kezdjük.
A 40 N-os erő függőleges, ezzel \(\displaystyle 35^\circ\)-os szöget zár be a \(\displaystyle T_1\) erő, illetve a \(\displaystyle T_2\) erő vízszintes. A szöget felmérve, majd a 40 N-os erő ellentettjét berajzolva, végül párhuzamosok berajzolásával leolvashatjuk, hogy \(\displaystyle T_1=49\,\mathrm{N}\) és \(\displaystyle T_2=28\,\mathrm{N}\).
A \(\displaystyle T_2=28\,\mathrm{N}\)-os erőt másoljuk át a jobb oldali csomópontba, és vegyük fel a függőleges irányú 50 N-os nehézségi erőt is. Ezek összege adja a \(\displaystyle T_3\) erő ellentettjét. A rajzról leolvashatjuk, hogy \(\displaystyle T_3=57\,\mathrm{N}\), illetve \(\displaystyle \vartheta=29{,}5^\circ\).
b) Durván azt mondhatjuk, hogy \(\displaystyle 0{,}5\,\mathrm{mm}\)-es pontossággal tudjuk az erőket leolvasni, ami 1%-os hibát jelent a nagyobb erők, illetve 2%-os hibát a kisebb erő esetében. A szöget fél fok pontossággal olvashatjuk le, ami a jelen esetben 2%-nál valamivel kisebb hibát jelent.
Megjegyzés. Szögfüggvények, illetve Pitagorasz-tétel segítségével is megkaphatjuk a kérdéses adatokat:
$$\begin{gather*} T_1=\frac{40\,\mathrm{N}}{\cos{35^{\circ}}}=48{,}83\,\mathrm{N}\qquad\Rightarrow\qquad\frac{\Delta T_1}{T_1}=3{,}5\cdot 10^{-3}=0{,}35\%,\\ T_2=40\,\mathrm{N}\cdot\tg{35^{\circ}}=28{,}01\,\mathrm{N}\qquad\Rightarrow\qquad\frac{\Delta T_2}{T_2}=3\cdot 10^{-4}=0{,}03\%,\\ T_3=\sqrt{T_2^2+(50\,\mathrm{N})^2}=57{,}31\,\mathrm{N}\qquad\Rightarrow\qquad\frac{\Delta T_3}{T_3}=5{,}4\cdot 10^{-3}=0{,}54\%,\\ \sin{\vartheta}=\frac{T_2}{T_3}=0{,}4887\qquad\Rightarrow\qquad\vartheta=29{,}26\,^\circ\qquad\Rightarrow\qquad\frac{\Delta\vartheta}{\vartheta}=8{,}3\cdot 10^{-3}=0{,}83\%. \end{gather*}$$Láthatjuk, hogy gondos szerkesztéssel a durva becsléssel megállapított hibahatárnál pontosabb eredményeket kaphatunk.
Statisztika:
A G. 882. feladat értékelése még nem fejeződött be.
A KöMaL 2025. márciusi fizika feladatai