Az I/S. 12. feladat (2016. november)

I/S. 12. Adott egy téglalap, melynek oldalai \(\displaystyle a\) és \(\displaystyle b\) hosszúak (\(\displaystyle 1\le a,b\le 10^{9}\) pozitív egész). Fedjük le hézagmentesen és átfedés, valamint kilógás nélkül a téglalapot a lehető legkevesebb számú csempével. Kétféle csempe van: az egyik típusú négyzet alakú, melynek oldalai \(\displaystyle 2^{k}\) hosszúak; a másik típusú téglalap alakú, melynek egyik oldalhossza \(\displaystyle 2^{k}\), másik pedig \(\displaystyle 2^{k+1}\) (\(\displaystyle 0\le k\le N\)).

Készítsünk programot is12 néven, amely kiszámítja, hogy legkevesebb hány csempét kell fölhasználni a lefedéshez. A program olvassa be a standard bemenet első sorából \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle N\) (\(\displaystyle 0\le N\le 30\)) értékét, majd írja a standard kimenet első sorába a minimálisan szükséges csempék számát.

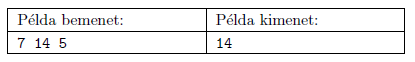
Magyarázat: a \(\displaystyle 7\times 14\)-es téglalap lefedhető egy \(\displaystyle 8\times 4\)-es, egy \(\displaystyle 4\times 4\)-es, négy \(\displaystyle 4\times 2\)-es, egy \(\displaystyle 2\times 2\)-es és hét darab \(\displaystyle 1\times 2\)-es csempével.

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. További 9 pontot ér, ha a program minden helyes bemenetet képes jól megoldani 1 mp futásidőkorláton belül. A programra kapható 9 pontból legföljebb 4 adható azokra a megoldásokra, amelyek csak az \(\displaystyle a, b \le 10^{3}\) nagyságú bemenetekre adnak helyes megoldást az időkorláton belül.

Beküldendő egy tömörített is12.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2016. december 12-én LEJÁRT.

A feladat megoldásával és a mohó algoritmus alkalmazhatóságával részletesen foglalkozunk a KöMaL 2017. márciusi számában.

A megoldások többsége mohó stratégiával dolgozott (kimondva, vagy kimondatlanul), illetve egy megoldás született dinamikus programozással.

Mintamegoldásként Janzer Orsolya Lili 11. évfolyamos budapesti (is12jol.cpp), Tóth Balázs 9. évfolyamos budapesti (is12tb.java), valamint Gáspár Attila 11. évfolyamos miskolci versenyző (is12ga.cpp) munkáját adjuk közre.

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Csenger Géza, Gáspár Attila, Horváth Botond István, Janzer Orsolya Lili, Kiss Gergely, Nagy Nándor, Németh 123 Balázs, Tóth 827 Balázs.
8 pontot kapott:	3 versenyző.
5 pontot kapott:	1 versenyző.

A KöMaL 2016. novemberi informatika feladatai