 |
Az I/S. 15. feladat (2017. február) |
I/S. 15. Benedek ásatásokon segédkezik, ahol az egyik nap találtak egy olyan szöveges dokumentumot, amelyben csak A és B betűkből álló, meglehetősen hosszú szavak szerepeltek. Benedek azt a feladatot kapta a főnökétől, hogy a szavak felett ívekkel, kettesével kösse össze az azonos betűpárokat (az A-t az A-val, a B-t a B-vel), majd számolja meg a dokumentumban szereplő ,,szép'' és ,,nagyon szép'' szavakat. ,,Szép''-nek nevezzük azokat a szavakat, amelyekben kialakítható olyan párosítás, amelynél minden egyes betűnek van párja és a rajzolt ívek nem keresztezik egymást. ,,Nagyon szép''-ek azok a szavak, amelyekben a szép kritériumnak megfelelő összekötés egyértelmű, vagyis pontosan egyféle a kereszteződés nélküli megfelelő összeköttetés.
A feladatunk a szövegben előforduló ,,szép'' és ,,nagyon szép'' szavak megszámolása.
A standard bemenet első sora a dokumentumon szereplő szavak \(\displaystyle N\) (\(\displaystyle 1 \le N \le 1\,000\)) számát, a következő \(\displaystyle N\) sor pedig a csupa A és B betűből álló szavakat tartalmazza. Egy-egy szó hossza legalább 1 és legfeljebb \(\displaystyle 100\,000\) betű. Az összes szó hosszának összege nem nagyobb, mint \(\displaystyle 1\,000\,000\). A standard kimenet első sorába a ,,szép'' szavak számát, míg a második sorába a ,,nagyon szép'' szavak számát kell írni.
Pontozás: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. További 7 pontot ér a ,,szép'' szavak számának helyes megadása, és további 2 pont a ,,nagyon szép'' szavak helyes megszámlálására jár.
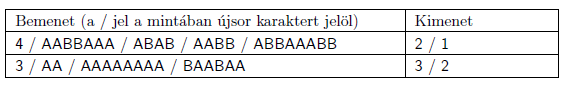
Magyarázat:
AABBAAA – nem szép és nem nagyon szép, mivel nincs minden betűnek párja;
ABAB – nem szép és nem nagyon szép, a betűk feletti párosítás metszi egymást;
AABB – szép és nagyon szép – az összekötés egyértelmű;
ABBAAABB – szép, de nem nagyon szép, mert az első A-t a 2. és a 4. A-val is lehet kötni, így többféleképpen is létrejöhet az átmetszés nélküli párosítás.
Beküldendő egy tömörített is15.zip állományban a program forráskódja és rövid dokumentációja, amely ismerteti a megoldás menetét és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2017. március 10-én LEJÁRT.
Statisztika:
13 dolgozat érkezett. 10 pontot kapott: Busa 423 Máté, Gáspár Attila, Nagy Nándor. 9 pontot kapott: Horváth Botond István, Molnár Bálint. 8 pontot kapott: 1 versenyző. 7 pontot kapott: 6 versenyző. 5 pontot kapott: 1 versenyző.
A KöMaL 2017. februári informatika feladatai

