 |
Az I/S. 18. feladat (2017. május) |
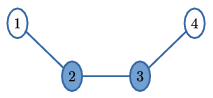
I/S. 18. Egy ország úthálózata \(\displaystyle N\) városból és bizonyos városokat összekötő kétirányú utakból áll. Bármely városból bármely másik városba el lehet jutni közvetlenül vagy közvetve. Egy áruházlánc újonnan érkezett az országba, és szeretne pontosan \(\displaystyle N/2\) áruházat építeni úgy, hogy minden városból legfeljebb egy szomszédos városig kelljen utazni, ha náluk szeretnénk bevásárolni. Más szóval, ha egy városban nem épül áruház, akkor legalább egy szomszédos városban kell majd építeni. Írjunk programot, amely megadja, hogy mely városokban legyen áruház.
A standard bemenet első sora a városok \(\displaystyle N\) számát és az utak \(\displaystyle M\) számát tartalmazza. A következő \(\displaystyle M\) sor mindegyike egy-egy út által összekötött két város sorszámát tartalmazza (a városokat 1 és \(\displaystyle N\) közötti egész számokkal azonosítjuk).
A standard kimenet első és egyetlen sora pontosan \(\displaystyle N/2\) azonosítószámot tartalmazzon, az építendő áruházak városainak sorszámát. Több megoldás esetén bármelyik megadható.
Korlátok: \(\displaystyle 2 \le N \le 100\,000\), páros szám; \(\displaystyle 1 \le M \le 1\,000\,000\). Időlimit: 1 mp; memórialimit: 256 MB.
| Minta bemenet (a \(\displaystyle \backslash\) jelek sortörést jelentenek) | Minta kimenet |
| 4 3 \(\displaystyle \backslash\) 1 2 \(\displaystyle \backslash\) 2 3 \(\displaystyle \backslash\) 3 4 | 2 3 |
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített is18.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2017. június 12-én LEJÁRT.
Statisztika:
10 dolgozat érkezett. 10 pontot kapott: Busa 423 Máté, Gáspár Attila, Janzer Orsolya Lili, Kiss Gergely, Molnár Bálint, Németh 123 Balázs, Noszály Áron. 7 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2017. májusi informatika feladatai

