Az I/S. 27. feladat (2018. május)

I/S. 27. Egy ország \(\displaystyle N\) városa között autóbuszjáratok közlekednek, melyeknek ismerjük a menetrendjét. A városokat pozitív egész számokkal jelöljük. Az 1-es városból szeretnénk eljutni az \(\displaystyle N\)-es városba autóbuszok segítségével. Minden járat két város között közlekedik, az egyes járatok azonos időközönként követik egymást. Tudjuk minden járatról a napi első indulási időpontot és a járat menetidejét. A járatok utolsó indulási ideje 20:00, később már nem indulnak autóbuszok. Az alábbi példa első járata az 1-es várostól a 4-es városig közlekedik, az út 80 percig tart, az első járat 7:00-kor indul (a nap 420. percében), majd minden következő 200 perccel az előző után, és így az utolsó 17:00-kor.

Átszálláskor legkorábban a megérkezés után legalább 10 perccel később induló buszokat érjük el biztonságosan. Minden városban van szálloda, így nem jelent gondot valamelyikben megszállni éjszakára. Számítsuk ki, hogy legkevesebb hány percig tart eljutni az induló városból a cél városba, illetve adjuk meg, hogy mely városokat érintünk egy ilyen utazás során. Ha több megoldás is lehetséges, akkor elég egyet megadni. A menetrend csak az eljutás szempontjából fontos járatokat tartalmazza, nem az összes járatot, de az 1-es városból biztosan el lehet jutni buszokkal az \(\displaystyle N\)-es városba.

A program a standard bemenet első sorából olvassa be a városok \(\displaystyle N\) számát, majd a következő \(\displaystyle N\) sorból a járatok induló és cél városát, a menetidőt, a nap első járatának indulási idejét 0:00-tól számítva, illetve az egymást követő buszok indulása közötti eltérés idejét percben. A program írja a standard kimenet első sorába a legrövidebb eljutás idejét percben, majd a következő sorba az egy ilyen időtartamú út során érintett városokat sorrendben.

Példa:

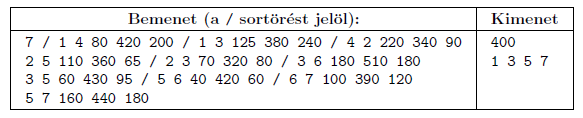
Korlátok: \(\displaystyle 4 \le N \le 100\), a menetidők nem hosszabbak 10 óránál.

Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb \(\displaystyle N\) értékek esetén ad helyes eredményt 1 másodpercen belül.

Beküldendő egy is27.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.

(10 pont)

A beküldési határidő 2018. június 11-én LEJÁRT.

Megoldásként Ürmössy Dorottya, 9. osztályos, budapesti versenyző megoldását mutatjuk be: dokuis27.txt, Program.cs.

A tesztelésként használt állományok és a helyes kimenetek: s125beki.zip.

Statisztika:

1 dolgozat érkezett.
10 pontot kapott:	Ürmössy Dorottya.

A KöMaL 2018. májusi informatika feladatai