 |
Az I/S. 28. feladat (2018. szeptember) |
I/S. 28. Egy hatalmas telken sportkomplexumot terveznek. A telekre gondolatban egy koordináta-rendszert helyeznek. A kialakítandó \(\displaystyle N\) darab sportpálya mind téglalap alakú, oldalaik a koordináta-rendszer tengelyeivel párhuzamosak. Ismerjük minden pálya két szemközti csúcsának koordinátáit. A pályáknak nincs közös területe, de oldalaik érintkezhetnek egymással. A tervek szerint két pálya között pontosan akkor készül majd átjáró, ha legalább \(\displaystyle D\) hosszú szakaszon érintkeznek egymással. Egy pálya egy oldalát a vele érintkező más pályák több szakaszra osztják (ha nem, akkor a teljes oldalt egy szakasznak tekintjük). Vegyük azokat a szakaszokat, amik a külső térre néznek, vagyis nem részei más pálya oldalának. Egy-egy ilyen, legalább \(\displaystyle D\) hosszú szakaszra bejáratot terveznek. Adjuk meg, hogy a sportkomplexum tervében összesen hány bejárat és hány átjáró van.
Bemenet: az első sor a pályák \(\displaystyle N\) számát és a \(\displaystyle D\) hosszúságot tartalmazza. A következő \(\displaystyle N\) sor mindegyike négy egész számot tartalmaz: egy-egy pálya két szemközti csúcsának koordinátáit.
Kimenet: egy sorba írjuk ki az átjárók, aztán a bejáratok számát.
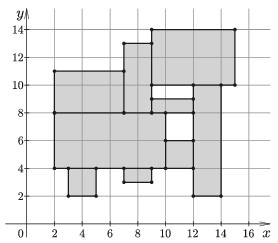
| Bemenet (a / jel sortörést helyettesít) | Kimenet |
| 9 2 2 8 10 4 / 7 13 9 8 / 9 9 12 8 / 10 6 12 4 / 12 10 14 2 9 14 15 10 / 2 11 7 8 / 3 4 5 2 / 7 4 9 3 |
9 22 |
Korlátok: \(\displaystyle 1\le N\le {10}^{5}\),
\(\displaystyle -{10}^{9}\le \text{koordináták}\le {10}^{9}\),
\(\displaystyle 1\le D\le {10}^{9}\), egész számok.
Értékelés: a pontok 20%-a kapható, ha \(\displaystyle D=1\); további 20% kapható, ha a pályák \(\displaystyle 1\times 1\)-es négyzetek; további 20% kapható, ha \(\displaystyle N\le 1000\); további 40% kapható az eredeti korlátokra.
Időlimit: 0,3 mp, memórialimit: 100 MiB.
Az I/S és S-jelű feladatok megoldását a http://mester.inf.elte.hu automatikus értékelő rendszer segítségével kipróbálhatod, tesztelheted (Téma: KöMaL - 2018/19).
(10 pont)
A beküldési határidő 2018. október 10-én LEJÁRT.
Statisztika:
12 dolgozat érkezett. 10 pontot kapott: Csertán András, Nagy Nándor, Noszály Áron, Szente Péter, Tóth 827 Balázs, Varga 256 Péter. 9 pontot kapott: Gyimesi Péter, Molnár Bálint. 5 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2018. szeptemberi informatika feladatai