Az I/S. 31. feladat (2018. december)

I/S. 31. Egy városban a parkokat kétirányú utcák kötik össze. Bármelyik parkból bármelyik parkba pontosan egy úton juthatunk el az utcákon sétálva. Két park távolsága legyen a közöttük levő útvonal utcáinak száma. Az összes parkpárra vett távolságok maximumát nevezzük \(\displaystyle D\)-nek. Ha két park távolsága \(\displaystyle D\), akkor a közöttük levő utat turistaútnak tekintjük. Egy park központi, ha a város összes turistaútvonala áthalad rajta. A város önkormányzata az összes központi parkba szuvenír boltot szeretne építeni. Adjuk meg a központi parkok számát és indexét.

Bemenet: az első sorban a parkok \(\displaystyle N\) száma (a parkok 0-tól \(\displaystyle (N-1)\)-ig vannak indexelve). A következő \(\displaystyle N-1\) sor mindegyike két park indexét tartalmazza, melyeket utca köt össze.

Kimenet: az első sorba írjuk ki a központi parkok számát, a következő sorba a központi parkok indexét növekvő sorrendben.

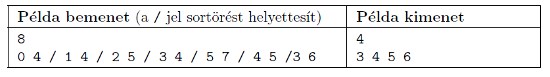
Korlátok: \(\displaystyle 2\le N\le {10}^{6}\).

Időlimit: 0,5 mp, memórialimit: 100 MiB.

Értékelés: a pontok 20%-a kapható, ha csak egy központi park van; további 20% kapható, ha \(\displaystyle N\le 100\); további 20% kapható, ha \(\displaystyle N\le 1000\); további 40% kapható az eredeti bemenetre.

Beküldendő egy is31.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy melyik fejlesztő környezetben futtatható.

Az I/S és S-jelű feladatok megoldását a http://mester.inf.elte.hu automatikus értékelő rendszer segítségével kipróbálhatod, tesztelheted (Téma: KöMaL - 2018/19).

(10 pont)

A beküldési határidő 2019. január 10-én LEJÁRT.

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:	Csertán András, Horcsin Bálint, Kiss Gergely, Molnár Bálint, Noszály Áron, Szente Péter.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.

A KöMaL 2018. decemberi informatika feladatai