Az I/S. 32. feladat (2019. január)

I/S. 32. Egy iskola könyvtárban összesen $\displaystyle M$ darab számítógép van. Egy nap $\displaystyle N$ diák előre megadta, hogy melyik időpillanattól melyik időpillanatig szeretne használni egy gépet. Tegyük fel, hogy egy diák az $\displaystyle a_{1}$ időpillanattól a $\displaystyle b_{1}$ időpillanatig szeretne gépezni, egy másik pedig $\displaystyle a_{2}$-től $\displaystyle b_{2}$-ig. Ők csak akkor használhatják ugyanazt a gépet, hogyha $\displaystyle b_{1}<a_{2}$ vagy $\displaystyle b_{2}<a_{1}$. Ha egy diák nem tud használni egy gépet sem a teljes kért időtartam alatt, akkor a könyvtárosnak el kell utasítania a kérését. Mivel csak $\displaystyle M$ gép van, így nem biztos, hogy mindenkinek lesz szabad gépe. A könyvtáros szeretne a lehető legkevesebb diáknak nemet mondani. Segítsünk neki egy programmal, amely megadja, hogy legkevesebb hány diáknak és kiknek kell nemet mondania.

Bemenet: Az első sor tartalmazza a diákok $\displaystyle N$ számát és a gépek $\displaystyle M$ számát. A diákokat 0-tól $\displaystyle N-1$-ig indexeljük. A következő $\displaystyle N$ sor mindegyike egy $\displaystyle a$ és egy $\displaystyle b$ számot tartalmaz, amely leírja, hogy az adott diák mettől meddig szeretne gépezni.

Kimenet: Az első sor tartalmazza azt a minimum számot, ahány diáknak nemet kell mondani. A következő sor tartalmazza azon diákok indexét növekvő sorrendben, akiknek nemet kell mondani. Több lehetséges megoldás, vagyis azonos számú elutasított diák esetén a legkisebb indexű diákokat fogadja a könyvtáros.

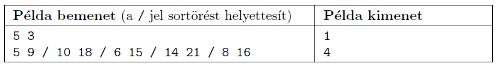
Korlátok: $\displaystyle 1\le N,M\le {10}^{5}$, $\displaystyle 0\le a,b\le {10}^{9}$, egy diákra: $\displaystyle a<b$.

Időkorlát: 0,5 mp.

Értékelés: A pontok 20%-a kapható, ha $\displaystyle N\cdot M\le {10}^{6}$; további 20% kapható, ha $\displaystyle b-a=1$ minden diákra; további 20% kapható, ha $\displaystyle a,b\le {10}^{6}$ minden diákra; további 40% kapható az eredeti korlátokra.

Beküldendő egy is32.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy melyik fejlesztő környezetben futtatható.

(10 pont)

A beküldési határidő 2019. február 11-én LEJÁRT.

Statisztika:

5 dolgozat érkezett.
10 pontot kapott:	Csertán András, Kovács Alex, Noszály Áron, Szente Péter.
8 pontot kapott:	1 versenyző.

A KöMaL 2019. januári informatika feladatai