Az I/S. 47. feladat (2020. október)

I/S. 47. Adél és Bence a következő játékot játsszák: Adél rajzol egy $\displaystyle N$ szélességű és $\displaystyle N$ magasságú egységoldalú négyzetekből álló négyzethálót, majd minden mezőbe beír egy egész számot. Ezután Bence választ egy $\displaystyle K$ pozitív egész számot, és rajzol egy $\displaystyle 3\cdot 3$ db, $\displaystyle K$ oldalhosszú négyzetekből álló hálót úgy, hogy $\displaystyle 3K\le N$ legyen. Ezután a saját $\displaystyle K$ oldalú négyzetei közül kiszínez tetszőlegesen $\displaystyle X$ darabot ($\displaystyle 1\le X\le 9)$, majd a saját mintáját ráilleszti a számozott négyzetrácsra úgy, hogy szélei a rácsvonalakra illeszkedjenek és a minta ne lógjon le a négyzetrácsról. Bence pontszáma a színezett terület által lefedett mezőkben lévő számok összege. Adjuk meg, hogy legföljebb hány pontot szerezhet Bence.

Bemenet: az első sor tartalmazza az $\displaystyle N$ számot. A következő $\displaystyle N$ sor mindegyike $\displaystyle N$ számot tartalmaz, a mezőkbe írt számokat. Az $\displaystyle i$-edik sor $\displaystyle j$-edik eleme $\displaystyle A_{i,j}$.

Kimenet: az elérhető legnagyobb pontszám.

Példa:

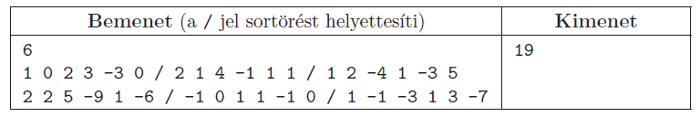
Korlátok: $\displaystyle 3\le N\le 100$, $\displaystyle -1000\le A_{i,j}\le 1000$, Adél biztosan írt nemnegatív számot. Időkorlát: 0,5 mp.

Értékelés: a pontok 50%-a kapható, ha $\displaystyle N\le 10$.

Beküldendő egy is47.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2020. november 16-án LEJÁRT.

Minden $\displaystyle i$, $\displaystyle j$, $\displaystyle K$ számhármasra megnézzük, hogyha $\displaystyle i$ az egyik, $\displaystyle j$ a másik koordinátája a bal felső saroknak, és a kis négyzetek oldala $\displaystyle K$, akkor mi a legjobb kiválasztás. Látható, hogy a $\displaystyle 3*3$ négyzet közül azokat kell kiválasztani, melyekben az összeg pozitív. Ezek közül a számítások közül kell a maximumot megkeresni.

Egy résztáblázatban (négyzetben) lévő számok összegének számítása $\displaystyle O(N^2)$-ről $\displaystyle O(1)$-re gyorsítható, ha minden mezőre eltároljuk a tőle balra felfelé lévő mezők összegét.

Komplexitás: $\displaystyle O(N^3)$

Statisztika:

11 dolgozat érkezett.
10 pontot kapott:	Horcsin Bálint, Varga 256 Péter.
9 pontot kapott:	Kovács Alex.
5 pontot kapott:	4 versenyző.
4 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. októberi informatika feladatai