Az I/S. 50. feladat (2021. január)

I/S. 50. Egy televíziós vetélkedő döntőjében két vagy három versenyző szerepel. A végső sorrendet közönségszavazással határozzák meg. Mindenki csak egy versenyzőre és legfeljebb egyszer szavazhat. A szavazás vége előtt öt perccel megmutatják az addig leadott szavazatok százalékos eloszlását. Pontosabban század százalékra kerekítve kiírják az állást anélkül, hogy megmondanák, melyik szám melyik versenyzőhöz tartozik.

Peti már biztosra tudja ki fog nyerni (a kedvenc versenyzője), így arra kíváncsi, mit tudhat meg még a számokból. Most azt szeretné megtudni, hogy legalább hányan adták le a szavazatukat a döntőben. Készítsünk programot, amely válaszol Peti kérdésére több ilyen vetélkedő esetén.

Bemenet: az első sor a vetélkedők, azaz a megoldandó esetek \(\displaystyle N\) száma. Ezután \(\displaystyle N\) sorban egy-egy lehetséges állás szerepel, mindegyikben legfeljebb három, a mintával megegyező formátumú szám.

Kimenet: a legkisebb szavazószám, amire igaz, hogy létezik olyan szavazateloszlás, amely a kiírt százalékos értékeket adja.

Korlátok: \(\displaystyle 1\le N\le 100\). Időkorlát: 0,1 mp.

Példa:

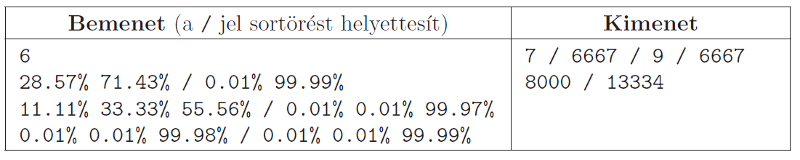
Figyelem: a kerekített számok összege nem feltétlenül ad 100%-ot.

Értékelés: A pontok 40%-a kapható, ha a döntőben két versenyzőre lehet szavazni. További 60% kapható, ha a versenyzők száma három.

Beküldendő egy is50.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2021. február 18-án LEJÁRT.

Legyenek kezdetben \(\displaystyle a=b=c=0\) és \(\displaystyle x=1\) Olyan \(\displaystyle x\)-et keresünk, melyre léteznek olyan \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) egészek, melyre \(\displaystyle a/x\), \(\displaystyle b/x\) és \(\displaystyle c/x\) megfelelően formázott (kerekített) értékei megegyeznek a bemenetben lévőkkel. Ehhez azt használjuk ki, hogy ha \(\displaystyle x\)-ről \(\displaystyle x+1\)-re növeljük a nevezőt, akkor a megoldáshoz legközelebb eső \(\displaystyle a, b, c\) számok nem változnak sokat.

Így az algoritmus: ha legközelebbi megoldásban (előző \(\displaystyle a,b,\) és \(\displaystyle c\)) valamelyik kerekített érték a bemenetben lévőnél nagyobb, akkor nincs ilyen \(\displaystyle x\)-el megoldás, így megnöveljük x-et. Ha ez nem igaz, akkor minden tört számlálóját addig növeljük, mígy a kerekített érték el nem éri a cél értéket. Ha egyik sem haladja meg azt, találtunk egy megoldást.

Mivel a 4 változó egyszerre növekszik, nem kell minden lehetőséget kipróbálni. Bizonyítható, hogy így biztosan megtaláljuk a legkisebb \(\displaystyle x\)-et.

A lebegőpontos számábrázolásból adódó pontatlanságok elkerüléséért egész számokat és maradékos osztást érdemes használni.

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Szakács Ábel.
9 pontot kapott:	Melján Dávid Gergő.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. januári informatika feladatai