Az I/S. 59. feladat (2022. január)

I/S. 59. Egy távoli országban egy hosszas havazás után \(\displaystyle D\) gyerek eldöntötte, hogy az egész napot hóemberépítéssel fogja tölteni. A nap végére el is készítettek \(\displaystyle N\) darab hógömböt. Az \(\displaystyle i\)-edik hógömb átmérője \(\displaystyle T[i]\) milliméter. Egy hóember építésekor tetszőleges számú hógömböt kell egymás tetejére tenni (egy hóember legalább két hógömbből áll), de figyelni kell arra, hogy egy hógömbre csak egy szigorúan kisebb hógömböt tehetünk.

Egy hóember szépsége \(\displaystyle H\), ha \(\displaystyle H\) darab hógömbből áll. A gyerekek megegyeztek, hogy mindegyikük pontosan egy darab H szépségű hóembert épít a hógömbök felhasználásával. Adjuk meg azt a legnagyobb \(\displaystyle H\) szépséget, amely esetén mindegyik gyerek tud egy \(\displaystyle H\) szépségű hóembert építeni a rendelkezésre álló hógömbökből.

A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle D\) számok találhatóak. A következő sor \(\displaystyle N\) darab számot tartalmaz, az \(\displaystyle i\)-edik szám \(\displaystyle T[i]\).

A kimenet egyetlen sorában egy szám szerepeljen: a legnagyobb elérhető \(\displaystyle H\) szépség. Ha nem lehetséges a megadott feltételek mellett legalább \(\displaystyle D\) azonos szépségű hóembert építeni, akkor a kimenet egyetlen sorában a \(\displaystyle -1\) szerepeljen.

Példa:

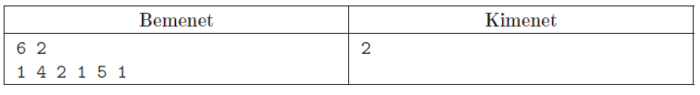
Nem építhető két darab 3 szépségű hóember, de 2 szépségű igen.

Korlátok: \(\displaystyle 1 \le N, D \le 100\,000\), \(\displaystyle 1 \le T[i] \le 10^{9}\). Időlimit: 0,4 mp.

Értékelés: a pontok 50%-a kapható, ha a program az \(\displaystyle 1 \le N \le 10\) tesztesetekre helyes megoldást ad.

Beküldendő egy is59.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2022. február 18-án LEJÁRT.

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:	Gyönki Dominik.
9 pontot kapott:	Kohut Márk Balázs, Nagy 292 Korina, Sándor Péter, Tóth 057 Bálint, Vadász Levente Márton, Veres Benedek Zoltán.
1 pontot kapott:	1 versenyző.

A KöMaL 2022. januári informatika feladatai