 |
Az I/S. 68. feladat (2023. január) |
I/S. 68. Adott egy \(\displaystyle N\)-jegyű pozitív egész szám. Egy lépés során kitörölhető egy számjegy az összes helyről, ahol előfordul, ha a visszamaradt szám pozitív szám marad, és nem kezdődik 0-val. Például egy lépés során a \(\displaystyle 33\,013\,211\) számból az 1-es számjegyek kitörlésével a \(\displaystyle 33\,032\) számot kapjuk, viszont a 3-as számjegyet nem lehet kitörölni, mert akkor a visszamaradt szám 0-val kezdődne. Hasonlóan a 777 számból sem törölhető ki a 7-es számjegy.
Adjuk meg, hogy legföljebb \(\displaystyle K\) törlés után melyik az a legkisebb szám, amit kaphatunk.
A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle K\) szám szerepel szóközzel elválasztva, a második sorban az \(\displaystyle N\)-jegyű szám szerepel.
A kimenet egyetlen sorában egyetlen szám szerepeljen: a legföljebb \(\displaystyle K\) törlés után megmaradt szám.
Példák:
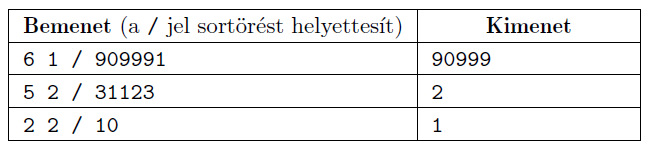
Korlátok: \(\displaystyle 1\le N, K\le 1000\). Időlimit: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha a program helyes kimenetet ad az \(\displaystyle N\le 9\) esetekben.
Beküldendő egy is68.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.
(10 pont)
A beküldési határidő 2023. február 15-én LEJÁRT.
Statisztika:
4 dolgozat érkezett. 10 pontot kapott: Nagy 292 Korina. 9 pontot kapott: Zádor-Nagy Zsombor. 5 pontot kapott: 2 versenyző.
A KöMaL 2023. januári informatika feladatai

