 |
Az I/S. 71. feladat (2023. április) |
I/S. 71. Egy étterem \(\displaystyle N\) asztallal rendelkezik, az \(\displaystyle i\)-edik asztal \(\displaystyle A[i]\) férőhelyes. Egy nap az étterembe \(\displaystyle M\) csoport érkezik, a \(\displaystyle k\)-adik csoport \(\displaystyle B[k]\) főből áll. Az étterem egy furcsa ültetési szokással rendelkezik: nem ülhet egy asztalnál két olyan ember, akik egy csoportból érkeztek. Adjuk meg, hogy legfeljebb hány csoport ültethető le teljesen az \(\displaystyle M\) csoport közül, ha egy asztalnál nem ülhet két azonos csoportból érkezett ember.
A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle M\) számok találhatóak szóközzel elválasztva, az asztalok és a csoportok száma. A második sorban \(\displaystyle N\) darab szám található szóközökkel elválasztva: a férőhelyek száma az egyes asztaloknál. A harmadik sorban \(\displaystyle M\) darab szám található szóközökkel elválasztva: az egyes csoportok létszáma.
A kimenet egyetlen sorában egy szám szerepeljen: a maximálisan leültethető csoportok száma.
Minták:
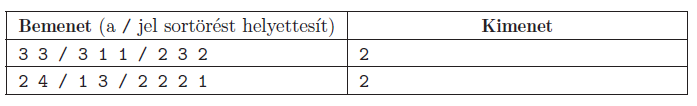
Magyarázat (1. példa): az első csoport embereit ültessük le az 1. és 2. asztalhoz; a 3. csoport embereit az 1. és 3. asztalhoz.
Korlátok: \(\displaystyle 1 \le N,M,A[i],B[i] \le 100\). Időkorlát: 0,4 mp.
Értékelés: a pontok 50%-a kapható arra a programra, amely helyes megoldást ad \(\displaystyle N=2\) esetén.
Beküldendő egy is71.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.
(10 pont)
A beküldési határidő 2023. május 15-én LEJÁRT.
Statisztika:
5 dolgozat érkezett. 10 pontot kapott: Gyönki Dominik, Nagy 292 Korina. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 2 versenyző.
A KöMaL 2023. áprilisi informatika feladatai