Az I/S. 72. feladat (2023. május)

I/S. 72. Egy levelibéka szeretne átjutni egy patak átellenes oldalára. A patak átellenes pontja, ahova a béka szeretne eljutni, \(\displaystyle M\) centiméterre van a béka jelenlegi pozíciójától. Szerencsére a patakon vízinövények élnek, melyekre ugorva könnyebb lehet az átkelés. A béka útjában összesen \(\displaystyle N\) számú vízinövény található (egyenes vonalban, a tó átellenes pontja felé), az \(\displaystyle i\)-edik vízinövény \(\displaystyle T[i]\) cm-re van a béka kiindulási helyétől.

A béka minden egyes másodpercben vagy szökken pontosan 1 cm-t (vagy a partra, vagy egy másik vízinövényre), vagy pedig ugrik legfeljebb \(\displaystyle D\) cm-t (vagy a partra, vagy egy másik vízinövényre). Az ugrás nagyon fárasztó, ezért minden ugrás után pihenésként szökkennie kell a békának (legalább egyszer).

Adjuk meg, hogy minimum mekkora \(\displaystyle D\) ugrásra kell képesnek lennie a békának, hogy át tudjon jutni a patak átellenes oldalára.

A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle M\) számok találhatók szóközzel elválasztva: a vízinövények száma, és a patak szélessége. A második sor szóközzel elválasztva tartalmaz \(\displaystyle N\) szigorúan monoton növekvő sorrendben adott számot: az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik növény \(\displaystyle T[i]\) távolsága a béka indulási helyétől.

A kimenet egyetlen sorában egy szám szerepeljen: a minimális \(\displaystyle D\) távolság, amivel a béka át tud jutni a túlpartra.

Minták:

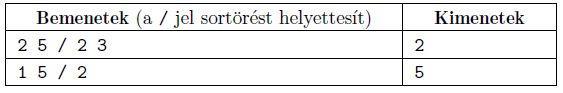
Magyarázat: az első példában a béka ugrik az 1. növényre, aztán szökken a 2. növényre, aztán ugrik a túlpartra. A második példában a béka egyből átugrik a túlsó partra (nem tudja felhasználni a növényt, mivel nem tudna szökkenni ugrás után).

Korlátok: \(\displaystyle 1\le N, M \le 10^5\), \(\displaystyle 0 < T[i] < M\), \(\displaystyle T[~]\) szigorú monoton növekvő. Időkorlát: 0,4 mp.

Értékelés: a pontok 50%-a kapható, ha a program helyes kimenetet ad az \(\displaystyle N,M \le 100\) esetekben.

Beküldendő egy is72.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

A beküldési határidő 2023. június 15-én LEJÁRT.

Statisztika:

4 dolgozat érkezett.
10 pontot kapott:	Gyönki Dominik, Horváth Milán, Szabó Imre Bence.
9 pontot kapott:	Zádor-Nagy Zsombor.

A KöMaL 2023. májusi informatika feladatai