Az I/S. 9. feladat (2016. május)

I/S. 9. Blöki \(\displaystyle N\) (\(\displaystyle 1\le N\le 10\)) érdekes pontot lát a síkon, melyeket meg akar látogatni. Blöki csak a koordinátatengelyekkel párhuzamos irányokban tud mozogni, és irányt csak az érdekes pontokon tud változtatni (akár vissza is fordulhat). Blöki dönthet úgy, hogy nem változtat irányt egy érdekes ponton, de úgy akarja az összes pontot meglátogatni, hogy útja során minden érdekes ponton pontosan egyszer változtat irányt: mondjuk azt, hogy ekkor vizsgálja meg az érdekes pontot. Blöki egy érdekes ponton akárhányszor áthaladhat, de pontosan egyszer akarja megvizsgálni. Útja során az összesen érdekes ponton át szeretne haladni, és a kiindulási pontba visszaérni. Blöki azon töpreng, hogy ezekkel a szigorú feltételekkel hányféleképp vizsgálhatja meg az összes pontot. Blöki egy ilyen körútja oda és vissza irányban két különböző útnak számít. Két körút különböző, ha különböző sorrendben vizsgálja Blöki az érdekes pontokat. Készítsünk programot, ami segít Blökinek megszámolni a megfelelő utakat. Blöki bármelyik pontból indulhat, az összes lehetőség érdekli.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et , majd a következő \(\displaystyle N\) sorból az érdekes pontok egész koordinátáit: \(\displaystyle -1000\le x, y\le 1000\). A program írja a standard output első sorába a lehetőségek számát.

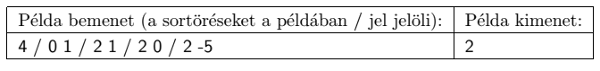
Magyarázat: a két útvonal: 1-2-4-3 és 3-4-2-1, Blöki mindkét esetben az origóból indul.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Beküldendő egy tömörített is9.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2016. június 10-én LEJÁRT.

Statisztika:

10 dolgozat érkezett.
10 pontot kapott:	Gáspár Attila, Gergely Patrik, Janzer Orsolya Lili, Molnár Bálint, Nagy Nándor, Németh 123 Balázs, Noszály Áron, Szakály Marcell.
3 pontot kapott:	2 versenyző.

A KöMaL 2016. májusi informatika feladatai