Az I. 110. feladat (2005. szeptember)

I. 110. Állítsuk elő az Euklides programmal, és vizsgáljuk meg a következő geometriai elrendezést. A csúcsai által adott egy ABC háromszög. A háromszög köré írt körön legyen D az A-t nem tartalmazó BC ív felezőpontja; hasonlóan kapjuk E és F pontokat. Legyen k₁ a D középpontú, BC oldalt érintő kör; k₂, k₃ az E és az F köré írható megfelelő kör.

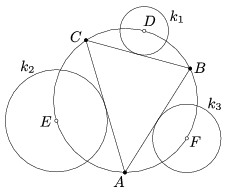
Rajzoljuk meg a k₁ és k₂, k₁ és k₃, illetve k₂ és k₃ körök külső közös érintőit! (Két-két érintő, összesen tehát 6 egyenes.) Milyen összefüggéseket figyelhetünk meg az így kialakult ábrán?

Beküldendő az ábra az Euklides saját formátumában (i110.euk), a geometriai megfigyelések pedig -- bizonyítás nélkül -- szöveg formájában (i110.txt, i110.rtf stb.). Az Euklides rajz pontosan három bázispontot tartalmazzon: A-t, B-t és C-t. A bázispontok bármely állásánál helyes kell, hogy maradjon az ábra, kivéve ha egyenlő szárú háromszöget határoznak meg, vagy egy egyenesre esnek.

(10 pont)

A beküldési határidő 2005. október 17-én LEJÁRT.

Megoldás.

A szerkesztés

Bár a szerkesztés nem túl bonyolult, de nem árt előre gondolni a diszkussziós problémákra, és a lehetséges szerkesztési eljárások közül olyat választani, ami a pontok tetszőleges elhelyezkedése mellett a helyes eredményt adja -- az Euklides-ben ugyanis sajnos nincs lehetőség a "program" elágazására, esetszétválasztásra.

Az első feladat megszerkeszteni az ívfelező pontokat. Ez elvégezhető az oldal felezőmerőlegesének és a körülírt körnek az elmetszésével, de ekkor sajnos bonyodalmak léphetnek fel az bázispontok fordított körüljárású, illetve tompaszögű eseteinél! A biztonságos megoldás pl. a belső szögfelező félegyenes és a körülírt kör elmetszése lehet. Bár nem nehéz felvenni a háromszög szögeit és megfelezni őket, a belső szögfelezők szerkesztésének sokkal egyszerűbb módja a beírt kör középpontjának felvétele és annak összekötése a csúcsokkal. (Ebből származott a legnagyobb bonyodalom, sok dolgozatban okozott diszkussziós problémákat, hogy az ívfelező pont néha a háromszögcsúcsot tartalmazó ívre került.)

ivfelezok.euk

A három kört felvehetjük pl. úgy, hogy megszerkesztjük egy kerületi pontjukat is. A legkézenfekvőbb a D, E, F pontokat merőlegesen levetíteni rendre a BC, CA, AB oldalakra, de ezzel egyenértékű az ABC oldalait elfelezni.

korok.euk

A szerkesztés legkényesebb pontja a közös külső érintők megkonstruálása. Ha valaki megsejti, vagy papíron készült vázlaton megfigyeli az ábra törvényszerűségeit, akkor nagyon egyszerűen felveheti az érintőket: például a "belső" helyzetűek az ABC beírt körének középpontján mennek át és rendre párhuzamosak az ABC oldalaival, míg a "külsők" az ABC köré írt kör érintői A-ban, B-ben, illetve C-ben. (Az ilyen szerkesztést teljes értékűnek tekintettük, mivel a feladat nem követelte meg a szerkesztés közvetlen voltát, vagy helyességének igazolását.)

Két általános diszjunkt kör közös külső érintőinek megszerkesztése nem annyira könnyű feladat (bár szerepel az Euklides példaszerkesztései közt, így ezt beemelve és makróként definiálva akár ezt is megoldhatjuk). A feladat feltételei azonban garantálják, hogy két szóba jövő kör különböző sugarú, és az ábrán több olyan irány is adódik, ami bizonyosan nem párhuzamos a centrális egyenessel. Így a centrális, valamint két hasonló helyzetű pontot összekötő egyenes [érintők.euk] metszéspontjaként adódik a két kör ún. külső hasonlósági pontja [A', B', C'], amiből közös érintő bocsátható a két körhöz.

A kész ábrát az i110.euk fájl tartalmazza.

i110.euk

Lehetséges megfigyelések

- A "belső" helyzetű közös külső érintők (amik a harmadik körhöz közel vannak) egy ponton mennek át: az ABC háromszög I beírt középpontján; valamint párhuzamosak a háromszög megfelelő oldalával. (Ezek az egyenesek részekre osztják a háromszöget; néhány versenyző a keletkező darabok közti területarányokról is megfigyeléseket tett.)

- A "külső" helyzetű közös külső érintők átmennek ABC megfelelő csúcsán, és érintik a körülírt körét.

- Az ábráról leolvasható a nevezetes Monge-D'Alembert tétel: a fent A', B', C'-vel jelölt három pont egy egyenesre esik (projektív értelemben is, ha az egyik az euklideszi síkon nem jön létre).

Az értékelésről

6 pont járt a helyes szerkesztésért, 4 pont pedig a geometriai megfigyelésekért.

Az előbbinél a diszkussziós problémák 1 pont levonást jelentettek (Ez jellemzően az ábra ABC körüljárására vagy tompaszögűségére való -- tiltott -- érzékenységét jelentette, de volt, hogy az ábra más instabil viselkedést is mutatott.) Néha a megoldás bonyolultsága miatt szinte lehetetlen megállapítani a helyes vagy téves működés eredetét, így mindez empirikus vizsgálattal került értékelésre.

Több esetben találkoztunk azzal a -- matematikailag téves -- elképzeléssel, hogy egy K és egy L kör egy közös külső érintőjének a K körrel vett P érintési pontját és a K kör középpontját összekötő szakasz merőleges a K és az L centrális egyenesével.

1 pontot az érintők helyes szerkesztése nélkül is meg lehetett szerezni, ha a k₁, k₂, k₃ körök a helyükön voltak.

A maximális pontszám eléréséhez legalább két nemtriviális megfigyelést vártunk el.

Rácz Béla András

Statisztika:

27 dolgozat érkezett.
10 pontot kapott:	Kacz Krisztián, Kiss Dániel Miklós, Ozsvárt László, Szolnoki Lénárd, Véges Márton, Vincze János.
9 pontot kapott:	Balambér Dávid, Czigler András, Dancsó Péter, Gilián Zoltán, Gombkötő Tamás, Gombos Gergely, Györök Péter, Kisfaludi-Bak Sándor, Kovács 129 Péter, Michael Swift, Ökrös Tamás.
8 pontot kapott:	3 versenyző.
6 pontot kapott:	1 versenyző.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2005. szeptemberi informatika feladatai