Az I. 111. feladat (2005. szeptember)

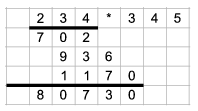
I. 111. Szemléltessük az írásbeli szorzást két háromjegyű szám összeszorzásán keresztül.

Készítsünk Excel táblázatot, melynek első sorába, meghatározott helyre két darab, háromjegyű egész számot írhatunk, számjegyenként külön cellába. A további sorokban jelenjen meg a két szám írásbeli szorzásának menete és a végeredmény. Feltételezhetjük, hogy a beírt számok valóban háromjegyűek, tehát például az első jegyük nem lehet 0.

Beküldendő a táblázat (i111.xls).

(10 pont)

A beküldési határidő 2005. október 17-én LEJÁRT.

Megoldás. A feladat megoldásához először is nézzük át az írásbeli szorzás menetét, így könnyebben kitalálhatjuk, hogy miként készítsük el a táblázatot.

Az első szám (szorzandó) minden számjegyét megszorozzuk a második szám (szorzó) éppen soron következő számjegyével. Az eredményt pedig leírjuk a szorzandó alá, megfelelő helyiértékkel eltolva. Az esetleges maradékot pedig először ,,megjegyezzük'', majd a következő két számjegy szorzásánál az eredményhez adjuk. A szorzó szájegyeit a legnagyobb helyiérték felől indulva vesszük, és ilyenkor a részszorzatokat mindig egyel jobbra tolva írjuk le. (természetesen lehet a legkisebb felől is indulni, de ekkor balra kell tolni a részszorzatokat). Végül ezeket a számokat összeadjuk az írásbeli összeadás szabályai szerint. Végighaladunk az oszlopokon, jobbról balra, és minden oszlopban a számok összegének utolsó jegyét leírjuk, a maradékot a következő helyiértékhez adjuk.

Excelben ezt könnyen megvalósíthatjuk, ha minden cellába olyan képletet írunk, melyben összeszorozzuk az ahhoz a cellához tartozó két számot, és hozzáadjuk az esetleges maradékot. A maradék kiszámítását pedig végezhetjük például egy rejtett cellában, de kiszámíthatjuk a következő két számjegy összeszorzásakor is.

Mivel eléggé külömböző képleteket kell írni a cellákba, így csak nagy bonyolultság árán lehetne egységes képletet írni, ezért egyszerübb, ha csak soronként általánosítjuk a számolást.

Én a következő képleteket írtam:

A MARADÉK függvényt az utolsó számjegy meghatározására használom, az INT függvénnyel pedig az átvitelhez számolom ki a maradékot. A pirossal írt számok a maradékok, ezek a megoldásban rejtett cellában vannak.

A feladatban megadott példában a háromjegyű részszorzatok elején nincsen 0 (pl: 0702), és papíron se írunk a számok elejére nullát. Ezért valahogy el kell tüntetni a pirossal karikázott helyeken a cella tartalmát, ha az nulla.

Erre egy lehetőség a feltételes formázás, melyet a Formátum/Feltételes formázás... alatt találunk. Beállítjuk ezekre a cellákra, hogy ha "A cella értéke" "egyenlő" "0" akkor fehér színnel írja ki a cella tartalmát, így az a fehér hátteren nem fog látszódni.

Egy másik megoldás, hogy ezekre a cellákra beállítunk egy egyéni formátumot, hogy 0 esetén üres cellával helyettesítse a 0-t. Ehhez írjuk be formátumnak a következőt: 0;-0;;@ (pozitív számokat kerekítse egészre ; negatív számokat kerekítse egészre ; 0-kat ne jelenítse meg ; szöveget ne módosítsa).

Harmadik megoldás, hogy a képletbe egy HA feltételt teszünk, pl: HA(F7=0;""; F7) , viszont ebben az esetben a cellára már nem hivatkozhatunk számként, tehát az esetek nagytöbbségében nem használható.

A feladatra 10 pontot azok kaptak, akiknek a megoldása minden esetben helyesen jelenítette meg a szorzás menetét. 8 pontot lehetett azért kapni, ha a sor elején a nullák megmaradtak, de a megoldás egyébként jó. Kevesebb pontot azok kaptak, akiknek valami komolyabb probléma miatt nem volt jó a megoldása, és csak bizonyos számokra adott jó eredményt. 0 pontot azok kaptak, akik nem a feladatkiírásban szereplő módon próbálták megoldani a feladatot.

Néhány jó tanács:

- Mielőtt beadtok valamit, ellenőrizzétek le több bemenetre is hogy jól müködik-e.

- Mindig próbáljatok a feladatkiírásban szereplő formához igazodni (pl sor elején nincs 0).

- Feladatmegoldás előtt gondoljátok végig, hogy ha papíron kellene megcsinálni számítógép nélkül, hogyan oldanátok meg. Így elkerülhető, hogy többsoros képleteket kelljen leírnotok egy egyszerü feladathoz.

Engedy István

* * *

A bemutatott megoldás letölthető innen.

Statisztika:

40 dolgozat érkezett.
10 pontot kapott:	Balambér Dávid, Bóra Eszter, Bőle Pál, Czigler András, Dancsó Péter, Deák Tibor, Fábián András, Fejér Attila, Gál Tibor, Gilián Zoltán, Gombkötő Tamás, Gulyás 990 Péter, Györök Péter, Horváth 151 Gábor, Kisfaludi-Bak Sándor, Kiss Dániel Miklós, Kovács 129 Péter, Ozsvárt László, Ökrös Tamás, Szoldatics András, Varga 842 Iván, Varga Attila József, Vecsey Dénes, Véges Márton, Vincze János.
8 pontot kapott:	10 versenyző.
6 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2005. szeptemberi informatika feladatai