 |
Az I. 114. feladat (2005. október) |
I. 114. Egy szigeten rókák és nyulak élnek. A nyulak -- szapora állatok lévén -- havonta m százalékkal lesznek többen. Egy róka minden hónapban elfogyasztja az összes nyúl p százalékát -- feltéve, hogy él ennyi nyúl ekkor a szigeten. A rókák a rendelkezésre álló táplálék arányában szaporodnak, minden hónapban nyulanként n százalékuk hoz világra kölyköt, miközben az összes róka q százaléka elpusztul.
Készítsünk Excel táblázatot, melybe beírva n, m, p és q értékét, illetve az állatok számát az első hónapban, hónapról hónapra kiszámolja az állatok számát a következő 60 hónap során. Ha időközben valamelyik (akár mindkét) faj kihalna, jelezze ezt a faj nevének pirosra színezésével. A táblázat mellé készítsünk két grafikont is, az egyiken a két faj populációját ábrázolva az idő függvényében, a másikon a két populáció arányát.
Beküldendő a táblázat (i114.xls).
Példa:
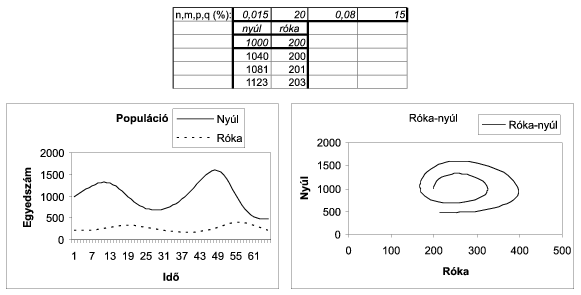
(10 pont)
A beküldési határidő 2005. november 15-én LEJÁRT.
Megoldás. A feladat megoldásának első lépése egy olyan képlet megírása, mely a nyulak és rókák előző havi példányszámából és a paraméterekből megadja az következő havi példányszámokat. Ehhez vegyük sorra a példányszámokat befolyásoló tényezőket (ny,r : a múlt havi számok, NY,R : az aktuális számok):
- A nyulak havonta m százalékkal lesznek többen: NY=(1+m/100)*ny
- Egy róka minden hónapban elfogyasztja az összes nyúl p százalékát: NY=-r*(ny*p/100)
- minden hónapban nyulanként a rókák n százaléka hoz világra kölyköt: R=(1+ny*n/100)*r
- havonta az összes róka q százaléka elpusztul: R=-(q/100)*r
így a képletek a következők:
NY=ny*(1+m/100-r*p/100); R=r*(1+ny*n/100-q/100).
(4 pont)
A képletek még tört és negatív számokat is adhatnak eredményül, viszont a példányszámok nemnegatív egész számok. Végezzük el a lefelé kerekítést,
NY=INT(ny*(1+m/100-r*p/100)); R=INT(r*(1+ny*n/100-q/100))
és ha az eredmény kisebb 0-nál akkor legyen az eredmény 0. Ezt megcsinálhatnánk egy HA() függvénnyel is, de használjuk inkább a MAX(...;0) függvényt:
NY=MAX(INT(ny*(1+m/100-r*p/100));0)R=MAX(INT(r*(1+ny*n/100-q/100));0)
A képleteket írjuk be a táblázatba, így megkapjuk az egyes hónapok pélányszámait. (2+1 pont)
A feladat szerint ha egy faj kihal, azt a nevének pirosra színezésével kell jelölni. Ezt a feltételes formázás segítségével tudjuk megtenni. Használhatunk segédcellákat, melyeknek róka és nyúl lesz az értéke akkor, ha kihal az adott faj. A cellákat pedig akkor színezzük, ha azok értéke megegyezik a segédcellákéval. Ez nem szép megoldás több okból is.
Ehelyett válasszuk ki a feltételes formázásnál a ,,A képlet értéke'' opciót. Ebben az esetben akkor lesz alkalmazva az adott formázás ha a beírt képlet értéke IGAZ. A súgó szerint egy olyan képletet kell megadni amely IGAZ vagy HAMIS értéket adhat. Ilyen például a $B$64=0 mely akkor igaz, ha a B64-es cella értéke 0 --- vagyis a nyulak (a B oszlopban vannak a nyulak) kihaltak a 60. hónapra. (ha előbb halnak ki, akkor is utána végig 0 marad a példányszámuk). (2 pont)
Ezután már csak a grafikon elkészítése maradt hátra. Ezt a ,,Diagram varázsló'' segítségével könnyen megtehetjük. Én a Grafikon/Vonal diagramtípust választottam.
Engedy István
Statisztika:
32 dolgozat érkezett. 10 pontot kapott: Balambér Dávid, Czigler András, Gilián Zoltán, Gombkötő Tamás, Györök Péter, Hunyady Márton, Kiss Dániel Miklós, Kovács 129 Péter, Kuslics Ferenc, Ozsvárt László, Pétercsák Richárd, Szakács Nóra, Szoldatics András, Vecsey Dénes. 9 pontot kapott: Biró 123 János. 8 pontot kapott: 5 versenyző. 6 pontot kapott: 6 versenyző. 5 pontot kapott: 4 versenyző. 4 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2005. októberi informatika feladatai

