 |
Az I. 120. feladat (2005. december) |
I. 120. S forint kölcsönt veszünk fel kamatos kamatra. A kamat havonta p százalék, a futamidő n hónap. A kölcsönt havonta, egyenlő részletekben fizetjük vissza; az első részletet az első, az n-edik részletet az n-edik hónap végén. A bank a törlesztőrészletek befizetése előtt tőkésít, azaz adósságunk a kamatlábnak megfelelő mértékben növekszik, ezután vonják le belőle a befizetett összeget, végül nemnegatív egészre kerekítik -- mindig felfelé.
Készítsünk OpenOffice vagy Excel táblázatot, ami összesítést készít adósságunk alakulásáról. A felhasználó az A2, B2 és C2 mezőkbe írja be a kölcsön induló összegét (S), a kamatlábat (p), illetve a futamidőt (n). Az E2 mezőben jelenjen meg a havi törlesztő összeg, a B oszlopban pedig az adósság alakulása az egyes törlesztések befizetése után. Az adósság változását a C4...F15 mezők helyén grafikonon is ábrázoljuk. Az első sor és oszlop mezőiben álljon magyarázat, hogy az alattuk, illetve melletük levő mező mit tartalmaz.
Példa:
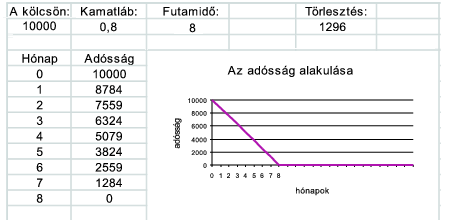
Beküldendő a táblázat (i120.sxc, i120.xls, ...). Feltételezhetjük, hogy n értéke legalább 3 és legfeljebb 24. A táblázat a kamatmentes kölcsönöket (amikor p=0) is kezelje helyesen.
(10 pont)
A beküldési határidő 2006. január 16-án LEJÁRT.
Megoldás. A feladatban a törlesztő részlet pontos kiszámítása okozta a legtöbb nehézséget.
Ha nem lenne kerekítés, a törlesztő összeg p=0 esetén , p
 0 esetén pedig
0 esetén pedig lenne.
A lefelé kerekítések miatt a helyes törlesztő részlet legalább ennyi. A t felső egész része logikus választás, de nem mindig helyes: a lefelé kerekítések miatt bizonyos esetekben a futamidő végén néhány forint adósság marad, ment minden hónapban elvesztünk egy 1 forintnál kisebb összeget. Akik ezt nem vették figyelembe, 8 pontot kaptak.
Ugyanakkor azt sem nehéz meggondolni, hogy ha a törlesztő részletet még 1 forinttal nagyobbnak választjuk, akkor minden hónapban legfeljebb akkora az adósság, mint a kerekítés nélküli esetben, ilyenkor tehát nem maradhat adósságunk.
Összefoglalva, kétféle érték közül kell választanunk. A legtöbb versenyző ezt úgy oldotta meg, hogy egy elrejtett oszlopban kiszámolta az adósság alakulását a kisebbik értékkel, és a táblázat látható részében az alapján választotta meg a törlesztő részletet, hogy a rejtett oszlopban maradt-e adósság a végén.
Fábián András (Szeged, Radnóti M. Kísérleti Gimn. és Ált. Isk, 9. o.) megoldása
Kacz Krisztián (Révkomárom, Selye János Gimn. 12.o.) megoldása
Vincze János (Debrecen, Fazekas M. Gimn. 11. o.) megoldása
Statisztika:
20 dolgozat érkezett. 10 pontot kapott: Czigler András, Kacz Krisztián, Vincze János. 8 pontot kapott: 5 versenyző. 7 pontot kapott: 5 versenyző. 6 pontot kapott: 1 versenyző. 5 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2005. decemberi informatika feladatai
|
|

