Az I. 164. feladat (2007. szeptember)

I. 164. A sejtautomata játék egy változatában a világot egy 27×27-es méretű négyzetrácsnak tekintjük, melynek mezőin sejtek élnek, egy mezőn legfeljebb kettő. A négyzetrács szélén lévő cellák érdekessége, hogy nekik is négy élszomszédjuk van: a felső sorban lévő cellák szomszédosak az alsó sor megfelelő celláival és viszont, hasonlóan a bal oldali oszlop cellái a jobb oldali oszlop celláival.

Szabályos időközönként új generációk jönnek létre. Minden sejt négyfelé osztódik, s ő maga elpusztul (egy-egy utód kerül a négy szomszédos cellák mindegyikébe). Ha egy cellába több utód is kerül, akkor azok hármasával elpusztítják egymást, amíg legfeljebb 1 vagy 2 marad.

Írjunk programot, amely a sejtek jelenlegi elhelyezkedése alapján meghatározza, hogy hogyan fog kinézni a világ N generáció múlva.

A program a szükséges adatokat a standard bemenetről olvassa. A bemenet első sora a generációk N () számát tartalmazza, az ezt követő 27 sor pedig rendre 27 számjegyet, a megfelelő cellákban élő sejtek számát (0, 1 vagy 2). Az eredményt a standard kimenetre írjuk, a bemenettel megegyező formátumban.

Ügyeljünk rá, hogy a program nagy N-ekre is gyorsan lefusson. Keressünk szabályosságot.

Helyszűke miatt itt egy kisebb (de minden más szempontból azonosan működő) példát közlünk:

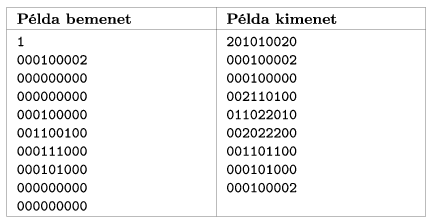
Egy teljes 27×27-es példa letölthető az Internetről.

Beküldendő a program forráskódja (i164.pas, i164.cpp, ...), valamint a program rövid dokumentációja (i164.txt, i164.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

27×27-es példa bemenet

27×27-es példa kimenet

(10 pont)

A beküldési határidő 2007. október 15-én LEJÁRT.

Megoldás

Mintamegoldásként Nagy Zoltán (Kaposvár, Munkácsy Mihály Gimnázium és Szakközépiskola, 11. osztály) C nyelven készült munkáját, illetve a hivatalos (C++ nyelven készült) mintamegoldást közöljük.

A szabályosság

A feladat szövegében több helyen utaltunk rá, az N-re vonatkozó korlátokkal és a holnapon szereplő tesztadattal implicite, a feladat szövegezésének végén pedig explicite, hogy a paraméterek ezen értékei mellett a játék valamilyen szabályosságot mutat.

Ahogy azt sokan jól észrevették, ez a szabályosság az volt, hogy a játéktér 27 generációnként periodikusan ismétlődött.

A matematikai igazoláshoz útmutatást nyújt Kós Géza "Kutyák a Marsról" című cikke, mely honlapunkon már régóta olvasható. Ott megmutattuk, hogy az osztódási eljárást végezhetjük minden egyes sejtre külön-külön, és a végén összegezhetjük az eredményeket maradékképzéssel, illetve, hogy a modulo 2 világban egy sejtnek 2^N lépésenként pontosan 4 utódja lesz, amelyek az eredeti sejttől fel, le, jobbra és balra helyezkednek el, mégpedig attól 2^N távolságra.

Hasonlóképp megmutatható, hogy a modulo 3 világban egy ezzel analóg szabály érvényes: 3^N lépésenként pontosan 4 utódja lesz minden sejtnek, az eredeti sejttől fel, le, jobbra és balra, attól 3^N távolságra. Mivel a játéktér 27 egység széles (és magas), ezt azt jelenti, hogy 3³=27 lépést végrehajtva egy sejt 4 utóda épp az őssejtnek megfelelő helyre kerül. Közülük hárman elpusztítják egymást, így összesen 1 marad. Mivel ez minden sejtre igaz, innen már rögtön adódik, hogy a játéktéren 27 lépést végrehajtva visszajutunk a kiindulási állapothoz.

Természetesen jóval egyszerűbb módon, próbálgatás útján is eljuthatunk ehhez a megfigyeléshez. Sőt, akár a programra is rábízhatjuk a feladatot: eltároljuk a kiindulási állapotot, és ha P lépés múlva ugyanaz áll elő, akkor megtaláltuk a periódust, a maradék N-P lépés helyett pedig csak annak P-re adott osztási maradékának megfelelő számút hajtunk végre.

A szabályosságot az utolsó teszteset megoldása során kellett kihasználni, ahol N=1000000000 volt. Ez a teszteset 2 pontot ért.

Típushibák, tanulságok

A problémák, a szabályosság fel nem fedezését nem tekintve, alapvetően három kategóriába sorolhatóak.

Nagyon sok megoldásban maradtak olyan, kisebb-nagyobb hibák, amelyeket a versenyzők egy kicsit több teszteléssel biztosan észrevettek volna, így azonban azt eredményezték, hogy a program a tesztesetek túlnyomó többségében helytelen eredményt produkált. Volt olyan megoldás is, amelyben 1 karakter elírása vezetett hibás működéshez, más programokban ezt egy tömb elindexelése, két ciklus felcserélése, illetve ehhez hasonló trivialitások okozták. A hiba nagyságától függően ezért 2-4 pontot vontunk le. Kérünk titeket, hogy a továbbiakban próbáljatok meg egy kicsivel több időt fordítani a program tesztelésére, élesztésére!

Néhány megoldás nem kezelte helyesen a specifikált tartomány határeseteit, ami jelen esetben az N=0 esetét jelentette. Ekkor természetesen a bemenetként kapott mátrixot kellett egy az egyben visszaadni.

A problémák legnagyobb része azonban specifikáció be nem tartásából származott. Noha ezért leggyakrabban nem, illetve kevés pontot vontunk le, kérjük, erre a továbbiakban sokkal jobban ügyeljetek!

Sok program a standard bemenet és kimenet használata helyett fájlból olvasta és fájlba írta az eredményt. Ezért 1 pont levonás járt.

Ezen kívül majdnem minden programnál volt valamilyen kisebb probléma a be- és/vagy kimenettel. Nagyon sok program extra szóközöket, újsorokat, elválasztó vonalakat, szövegeket írt ki, a futás végén billentyűleütésre várt. Amennyiben a feladat szövegében a be- és kimenetet pontosan definiáljuk, úgy a program a bemenetet mindig a specifikált formában fogja kapni, így azt nem kell ellenőrizni, illetve a kért kimeneten kívül semmi mást nem kell kiírni.

A specifikáció pontos betartására azért van szükség, mert a javítást - legalábbis a program helyes működésének ellenőrzését - igyekszünk automatizálni. Ez viszont csak úgy lehetséges, ha a programokat egységes módon tudjuk lefuttatni a tesztadatokra: azaz ha a program külön felhasználói beavatkozás nélkül képes beolvasni a bemenetet, a kimenetben a specifikált formátumban szerepelnek a kért adatok, illetve ezen túl semmi más nem szerepel. Kérünk titeket, hogy a megoldás során használt debug információk kiírását, illetve a billentyűleütésre várakozásokat is legalább kommentezzétek ki!

Engedy Balázs

cell.cpp

nagy.zip

Statisztika:

21 dolgozat érkezett.
10 pontot kapott:	Adrián Patrik, Juhász Péter, Nagy Zoltán, Véges Márton.
9 pontot kapott:	Hodosy Gábor.
8 pontot kapott:	4 versenyző.
7 pontot kapott:	5 versenyző.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	2 versenyző.
4 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2007. szeptemberi informatika feladatai