Az I. 198. feladat (2008. november)

I. 198. Szimuláljuk táblázatkezelő segítségével egy vízszintes, egyenletesen forgó korong közepéről elindított m tömegű test mozgását. A korong az óramutató járásával ellentétes irányban forog függőleges szimmetriatengelye körül, bármely pontjának v_k sebessége (ún. kerületi sebessége) a középpontból az adott pontba húzott egyenesre merőleges irányú, nagysága a középponttól mért távolsággal egyenesen arányos. A pontszerűnek tekinthető, m tömegű testet a korong középpontjából indítjuk V₀ kezdősebességgel, majd magára hagyjuk. A testre ezután (vízszintesen) csak a korong által kifejtett állandó nagyságú F_s csúszási súrlódási erő hat, melynek iránya ellentétes a test koronghoz viszonyított sebességével.

Vizsgáljuk a folyamatot egy olyan derékszögű koordináta-rendszerben, melynek origója a korong középpontja, és az x tengely V₀ irányába mutat. A szimulációt úgy végezzük, hogy a folyamatot t nagyságú időközökre osztjuk, mely időközökön belül a vizsgált fizikai mennyiségeket állandónak tekintjük. A kiindulási állapot után bármely időpont aktuális értékeiből a t-vel későbbi időpont értékeit a következő módon számítjuk ki:

a test helyzetét leíró x és y koordinátákat minden esetben az előző időszak v_x és v_y sebességkoordinátáinak t-szeresével növeljük;

kiszámítjuk a test középponttól mért r távolságát, valamint a korong adott pontbeli sebességének vk_x és vk_y összetevőit;

kiszámítjuk a korong testtel érintkező pontja és a test sebességvektorainak különbségét, mivel ezzel egyező irányú lesz a testre ható súrlódási erő;

kiszámítjuk a súrlódási erő komponenseit, majd a segítségükkel a gyorsulások koordinátáit;

a gyorsulások komponenseit t-vel szorozva megkapjuk a sebességváltozásokat: ezekkel növeljük a következő szimulációs lépésben a sebességet.

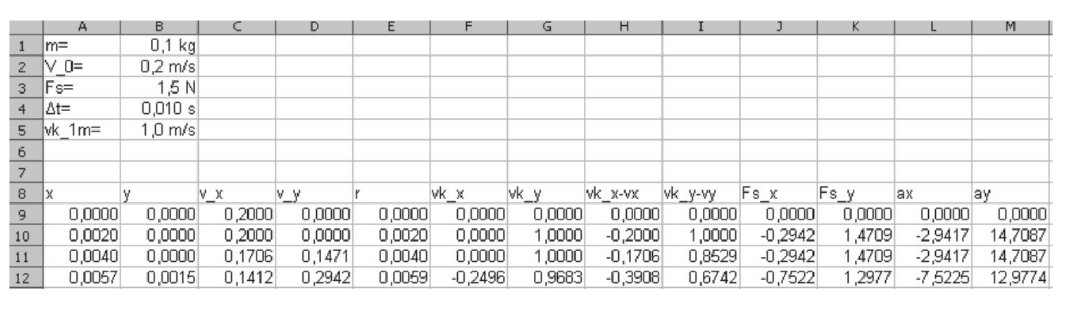
A test tömegét, a kezdeti sebességet, a súrlódási erő nagyságát, a szimulációs lépések között eltelt időt és a korong középponttól 1 méterre lévő pontjának kerületi sebességét a táblázat első öt sorában adjuk meg a mintának megfelelően. A táblázat további soraiban a test mozgását leíró mennyiségek legalább 300 értékét számítsuk ki, és a mozgás pályáját ábrázoljuk megfelelő diagramon.

Beküldendő a táblázatkezelő munkafüzet (i198.xls, i198.ods, ...), illetve egy rövid dokumentáció (i198.txt, i198.pdf, ...) amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.

(10 pont)

A beküldési határidő 2008. december 15-én LEJÁRT.

Legyen a munkalapon a kezdeti értékek elrendezése a mintának megfelelően az A1:B5 tartományban. A szimuláció adatait tartalmazó táblázat értékeit minden második és azt követő sorban az előző és az adott sorra való hivatkozásokat tartalmazó képletekkel tudjuk kiszámítani. Amennyiben a táblázat fejléce a munkalap 8. sorában van, a kiindulási értékeket a 9. sorban találjuk, akkor a másolható képletek a 10. sortól kiindulva az alábbiak szerint alakulnak:

Az előző állapotbeli hely értékét változtatjuk az előző állapotban fölvett sebességkoordináták és az eltelt idő szorzatával, azaz A10=A9+C9*B$4 és B10=B9+D9*B$4.

A gyorsulások előző értékei és az eltelt idő szorzatával növeljük a sebességkomponenseket, tehát C10=C9+L9*B$4 és D10=D9+M9*B$4.

Pitagórasz tételével kiszámítjuk a test távolságát a korong középpontjától, azaz E10==GYÖK(A10²+B10²).

A korong az óramutató járásával ellentétes irányban forog, a test helyén lévő pontjának kerületi sebessége merőleges a test helyvektorára, így iránya a (-y/r,x/r) egységvektorral egyező. A sebességvektor nagysága 1méter sugárnál a B5 cellában található érték, r sugár mellett éppen r és B5 szorzata. A sebességkomponensek képletéből az r sugár kiesik, így F10==-B10*B$5 és G10=A10*B$5.

A súrlódási erő a test és a korong egymáshoz viszonyított elmozdulásából számítható, ezért megadjuk a sebességvektoraik különbségét, így H10=F10-C10 és I10=G10-D10. A súrlódási erő nagysága állandó, a B3 cellában található érték, iránya az előbb kiszámított sebességkülönbséggel egyező. Készítsünk egységvektort tehát a sebességek eltéréséből és szorozzuk B3-mal: J10=H10/GYÖK(H10²+I10²)*B$3 és K10=I10/GYÖK(H10²+I10²)*B$3.

A gyorsulás vektorának komponensei Newton II. törvénye alapján a test vízszintes mozgását egyedül meghatározó súrlódási erő és a tömeg hányadosaként kaphatóak, azaz L10=J10/B$1 és M10=K10/B$10.

A képletek a következő sorokba egyszerűen másolhatók. Az első számításokat tartalmazó sor kiindulásként a (0;0) koordinátákat és a kezdeti X irányú sebességet tartalmazza, tehát A9=B9=D9=0 és C9=B2. A többi cella a 10 sorba írt képletekből másolható.

A számítással kapott helyzet koordinátákat érdemes jelölők nélküli, görbített vonallal összekötött Pont(XY) diagramon ábrázolni.

Egy Excelben készült mintamegoldást mellékelünk: i198mo.xls.

Statisztika:

16 dolgozat érkezett.
10 pontot kapott:	Balla Attila, Englert Péter, Földes Imre, Szabó 928 Attila.
9 pontot kapott:	Fehér Péter, Horváth 135 Loránd, Nagy 111 Miklós, Uray Marcell János.
7 pontot kapott:	1 versenyző.
6 pontot kapott:	3 versenyző.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2008. novemberi informatika feladatai