Az I. 217. feladat (2009. szeptember)

I. 217. A kristályosodás folyamatát és eredményét például az itt leírt módon vizsgálhatjuk. Legyen N kristályosodási góc egy M×M-es, olvadt anyagot tartalmazó reakciótérben. Az olvadékot fehér és minden növekvő kristályt más szín jelöl. A kristályosodás a már kivált (színes) kristály felszínén megy végbe, tehát a kristály reakciótérbeli oldalszomszédai felé folytatódik. Minden kristály azonos sebességgel, 1 réteggel nő lépésenként.

Az 1. ábrán egy példa látható a kristályok növekedésére 3 lépés után.

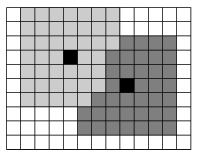
1. ábra

A kristályosodás folyamatának párhuzamosságát azzal biztosítjuk, hogy minden lépésben az összes növekvő kristályt megvizsgáljuk, és ha lehetséges, a felszínükre újabb réteg válik ki. Csak az olvadt anyag tud kristályosodni, a kivált anyag már nem változhat.

Készítsünk szimulációs programot, amely N (3N15) kristályosodási gócot véletlen helyre elhelyez az M×M (10M600) reakciótérben. A kristályok véletlenszerűen választott színnel növekedjenek ott, ahol még olvadék van. A szimuláció addig tartson, ameddig az összes olvadék ki nem kristályosodik.

Egy lehetséges eredmény látható a 2. ábrán.

2. ábra

Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más, a fordító által generált kiegészítő állományok nélkül) egy tömörített mappában (i217.zip).

(10 pont)

A beküldési határidő 2009. október 12-én LEJÁRT.

Megoldásokról

Több olyan megoldás érkezett, amely formájában nem felelt meg a Versenykiírásnak. A téves állománynév, a tömörítés hiánya, a dokumentáció vagy komment hiánya egy-egy pontveszteséget jelentett.

Horváth 135 Loránd 12. osztályos (Budapest, Németh László Gimnázium) megoldása alapján közöljük:

Ha elképzeljük lépésenként a szimulációt, akkor azt látjuk, hogy a tömbben adva van néhány góc, azaz tömbelem. A tömbelem köré a kristályosodás következő lépésekor keletkezik egy keret. A keret vastagsága megegyezik azzal a számmal, ahányadik lépésnél tartunk.

A szimuláció minden lépésében egy ”keretet vonok” a már meglévő rész köré. A tömböt feldolgozás előtt feltöltöttem csupa nullával, ez jelképezi az olvadékot. Ahol már kikristályosodott az anyag, ott nullától eltérő szám van, ami az adott rész színét írja le.

Feldolgozáskor mindig csak abba a tömbelembe írok, ami eddig 0 volt. Így kialakulnak a kristályosodási határok anélkül, hogy valami ”belelógna” a másikba.

A keret rajzolása két lépésből áll: A keret vízszintes részeit, majd a függőleges részeket rajzolom meg egy ciklusban.

Ha az i-edik gócpont koordinátái a goc[i].x és a goc[i].y, akkor a keret felső része az n-edik lépésben a következő lesz:

(goc[i].x-lepes, goc[i].y-lepes) ...(goc[i].x+lepes, goc[i].y-lepes) Például a második lépésben a goc[i].x-2-től a goc[i].x+2-ig kell vonni egy keretet: A szimuláció addig tart, ameddig az összes olvadék ki nem kristályosodik, amíg az olvadek logikai változó értéke hamis nem lesz Ezután kirajzolom a szimuláció eredményét.

Mintamegoldás

Janosov Milán 12. osztályos (Veszprém, Lovassy László Gimnázium) programja i217A.pas

Statisztika:

16 dolgozat érkezett.
10 pontot kapott:	Balla Attila, Barta 111 János, Bostyai Marcell, Fejes Márk, Giczi Dániel, Horváth 135 Loránd, Janosov Milán.
9 pontot kapott:	Mészöly Dániel Máté, Pap 999 Dávid, Szabó 928 Attila.
8 pontot kapott:	2 versenyző.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2009. szeptemberi informatika feladatai