 |
Az I. 264. feladat (2011. március) |
I. 264. Az ún. kerekítési lemma kimondja, hogy bármely olyan valós elemű mátrixhoz, melynek minden sor- és oszlopösszege egész, létezik egy -- ugyanazokkal a sor- és oszlopösszegekkel rendelkező -- olyan mátrix is, melynek minden eleme is egész, sőt, minden eleme az eredeti mátrix megfelelő elemének alsó vagy felső egész része.
A lemma bizonyítása meglepően egyszerű, és algoritmust is ad az egész elemű mátrix elkészítésére.
Ha az eredeti mátrix csupa egész elemekből áll, akkor készen vagyunk, ellenkező esetben vegyük egy tetszőleges nem egész elemét. Mivel a sorösszegek egészek, ennek sorában biztosan van még egy nem egész elem, amelynek oszlopában pedig -- az egész oszlopösszegek miatt -- van egy harmadik, melynek sorában egy negyedik, és így tovább.
A nem egész elemeken ily módon -- azaz a sorok, illetve oszlopok mentén felváltva -- lépkedve, és közben a meglátogatott elemeket megjelölve, egyszer csak egy olyan sorba vagy oszlopba ütközünk, amelyben már jártunk. Ebben sétánk korábbi szakaszából pontosan két megjelölt mátrixelem lesz: egy, amelyen keresztül először megérkeztünk a kérdéses sorba vagy oszlopba (ezt jelölje x), és egy másik, amellyel elhagytuk azt (z). Ezen kívül van még természetesen a harmadik, ,,problémás'' mátrixelem (p), amelyen keresztül ismét megérkeztünk a korábban már látogatott sorba vagy oszlopba (ez esetleg egybeesik x-szel).
Tekintsük most a séta ütközés utáni részéből képzett körsétát, tehát azt, amely z-vel kezdődik és p-ben ér véget (lásd: példa). Könnyen látható, hogy ez a körséta páros hosszú, és minden érintett sorból és oszlopból pontosan 2 megjelölt mátrixelemet tartalmaz, mégpedig egymás után. Így amennyiben a körséta minden eleméhez felváltva hozzáadunk, illetve kivonunk egy  konstanst, a sor- és oszlopösszegek nem változnak.
konstanst, a sor- és oszlopösszegek nem változnak.
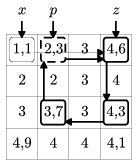
Példa: Amennyiben a bal felső sarokból indulunk, és a nem egész mátrixelemeket az a11, a14, a34, a32, a12 sorrendben kezdjük el meglátogatni, az 4. lépés után (p=a12) jutunk először már meglátogatott sorba (x=a11, z=a14). A bejárás ütközés utáni szakaszából kapott körséta tehát: a14, a34, a32, a12.
Ezt a  konstanst válasszuk úgy, hogy a megjelölt mátrixelemek és a hozzájuk legközelebb eső egész számok közti különbségek abszolút értékeinek minimuma legyen (a megfelelő előjellel). Ekkor a hozzáadásokkor és kivonásokkor egyik mátrixelem sem ,,csordulhat túl'' a saját felső vagy alsó egész részén, és legalább eggyel csökken a nem egész elemek száma. Amennyiben pedig még ez után is marad nem egész elem, úgy az egész eljárást ismételjük meg.
konstanst válasszuk úgy, hogy a megjelölt mátrixelemek és a hozzájuk legközelebb eső egész számok közti különbségek abszolút értékeinek minimuma legyen (a megfelelő előjellel). Ekkor a hozzáadásokkor és kivonásokkor egyik mátrixelem sem ,,csordulhat túl'' a saját felső vagy alsó egész részén, és legalább eggyel csökken a nem egész elemek száma. Amennyiben pedig még ez után is marad nem egész elem, úgy az egész eljárást ismételjük meg.
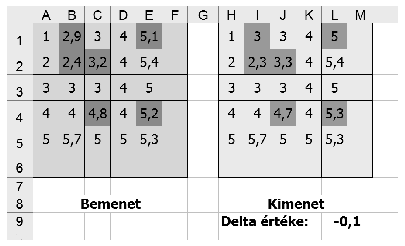
Készítsünk táblázatot, mely a fenti algoritmus egyetlen iterációját hajtja végre: a bemeneti és kimeneti mátrix, illetve  értéke az ábrán láthatóhoz hasonló módon helyezkedjen el (de a megoldásban legalább 10×10-es mátrixoknak biztosítsunk helyet!), a megjelölt mátrixelemeket mindkét mátrixban feltételes formázással emeljük ki. Több lehetséges megoldás esetén bármelyik megadható.
értéke az ábrán láthatóhoz hasonló módon helyezkedjen el (de a megoldásban legalább 10×10-es mátrixoknak biztosítsunk helyet!), a megjelölt mátrixelemeket mindkét mátrixban feltételes formázással emeljük ki. Több lehetséges megoldás esetén bármelyik megadható.
A feladatot táblázatkezelő függvényekkel, makrók használata nélkül kell megoldani, a mellékszámításokról részletes magyarázatot várunk.
Beküldendő a táblázatkezelő munkafüzet (i264.xls, i264.ods, ...), illetve egy rövid dokumentáció (i264.txt, i264.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma, valamint a megoldás leírása.
(10 pont)
A beküldési határidő 2011. április 11-én LEJÁRT.
Megoldás
Mintamegoldásként közöljük Szabó Attila (Pécs, Leőwey Klára Gimn.) munkáját, amely OpenOffice 2.1-gyel készült.
Statisztika:
4 dolgozat érkezett. 10 pontot kapott: Szabó 928 Attila. 7 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2011. márciusi informatika feladatai
|
|

