Az I. 274. feladat (2011. október)

I. 274. Adott egy n×m-es (1n,m500) téglalap alakú terület, amely fekete és fehér négyzetekből áll. Keressük meg ebben azt a legnagyobb téglalapot, amely csak fehér cellákat tartalmaz. Az eredményt a téglalap bal felső és jobb alsó sarkának a koordinátáival és a területével adjuk meg.

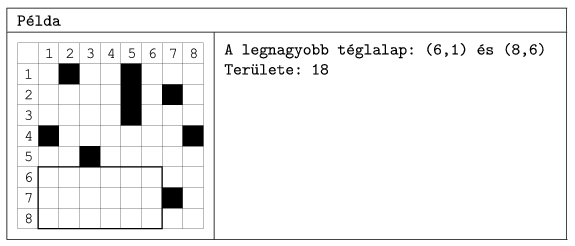
Érdemes meggondolni, hogy n és m viszonylag kis értéke mellett használható módszer, hogy az összes koordináta-párral meghatározott valamennyi téglalap fekete cella-mentességét egymásba ágyazott ciklusokkal ellenőrizzük, majd ezekből a maximális területűt kiválasztjuk. Az összehasonlítások száma az elemek számának negyedik hatványával lesz arányos és ez a futási időt az elemszám növelésével rendkívül megnöveli.

Megoldási ötlet: Számítsuk ki előre és tároljuk el minden cellához, hogy a terület bal felső sarkával együtt téglalapot alkotva hány fekete cellát tartalmaz.

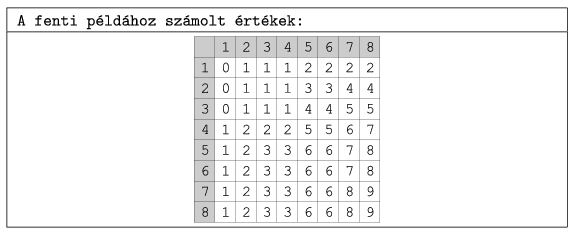
Az így előkészített értékekkel két koordináta-párral megadott téglalap fekete cella-tartalma ciklusok nélkül kiszámítható.

Készítsünk programot i274 néven, amely meghatározza a legnagyobb téglalapot, amely csak fehér cellákat tartalmaz.

A program a terület nagyságát és a cellák színét (0: fehér és 1: fekete) fájlból olvassa be. A fájl első sora a sorok számát (n) és az oszlopok számát (m) adja meg. Az ezt követő n darab sorban szereplő m darab érték, a példa szerint szóköz elválasztása nélkül, pedig a megfelelő cellák állapotát (0 vagy 1) írja le.

Az eredményt, azaz a téglalap bal felső és jobb alsó sarkainak koordinátáit és a téglalap területét a képernyőn jelenítjük meg. A program egyetlen parancssori argumentuma a bemeneti fájl legyen. A program futtatási ideje maximum 60 másodperc a tesztelésre használt 2.40 GHz, Core2Duo processzorú számítógépen.

Beküldendő egy tömörített i274.zip állományban a program forráskódja (i274.pas, i274.cpp, ...) és a program rövid dokumentációja (i274.txt, i274.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2011. november 10-én LEJÁRT.

Megoldásokról:

Viszonylag sok, teljes értékű megoldás érkezett. A megoldók egy része nem használta a feladat szövegében megfogalmazott ötletet, hogy előre számítsuk ki és tároljuk el minden cellához, hogy a terület bal felső sarkával együtt téglalapot alkotva hány fekete cellát tartalmaz. Az így előkészített értékekkel két koordináta-párral megadott téglalap fekete cella-tartalma ciklusok nélkül kiszámítható.

Többen észrevették, hogy az egyes cellákhoz tartozó fekete négyzetek számát rekurzív módszerrel meg lehet határozni:

Ha (a,b) cella fekete, akkor T(a,b)=T(a-1,b)+T(a,b-1)-T(a-1,b-1)+1. Ha a cella fehér, akkor T(a,b)=T(a-1,b)+T(a,b-1)-T(a-1,b-1).

A T(0,b)=0 és T(a,0)=0, minden a-ra és b-re.

Ha egy téglalap bal felső sarka (a1,b1) és a jobb alsó sarka (a2,b2) és nincs benne fekete cella, akkor: T(a2,b2)=T(a1-1,b2)+T(a2,b1-1)-T(a1-1,b1-1). Az algoritmus egymásba ágyazott ciklusok segítségével mindig egy adott cellából kiinduló téglalapokat vizsgálja, majd a nem fekete cella tartalmúak közül a legnagyobbat választja ki.

Mintamegoldásként Szilágyi Dániel 10. osztályos (Újvidék, Jovan Jovanovic Zmaj Gimnázium) tanuló munkáját közöljük: I274.cpp

A megoldások vizsgálatához használt tesztállományok: teszt.zip

A tesztállományok nevei, egyik legnagyobb téglalap két koordinátája, amely csak fehér cellákat tartalmaz és ennek területe:

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Adrián Patrik, Antal János Benjamin, Barkaszi Richárd Miklós, Fényes Balázs, Gema Barnabás, Hoffmann Áron, Jákli Aida Karolina, Kovács Balázs Marcell, Kucsma Levente István.
9 pontot kapott:	Varga 256 Erik.
8 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.

A KöMaL 2011. októberi informatika feladatai