Az I. 289. feladat (2012. március)

I. 289. Gyermekkorunk egyik kedvelt játéka a dominó. Minden dominólap két nem negatív egész számból, illetve a két számnak megfelelő számú pöttyből áll. Egy \(\displaystyle N\) nagyságú (\(\displaystyle 0\le N\le 10\)) készletben minden szám 0 és \(\displaystyle N\) közötti. Két dominólap megegyezik, ha rajtuk a számok az olvasási sorrendtől függetlenül azonosak. Egy dominókészlet nem tartalmaz azonos dominókat.

Pédául egy 2-es dominókészlet a következő dominókat tartalmazza: [0 0] [0 1] [0 2] [1 1] [1 2] [2 2].

Első feladatunk, hogy állítsunk elő funkcionális algoritmussal az \(\displaystyle N\)-es dominókészletet. Az előállítást végző függvény bemenete \(\displaystyle N\) értéke, eredménye a dominólapok alábbi minta szerint rendezett sorozata.

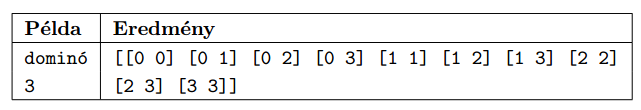
Második feladatunk, hogy készítsünk függvényt, amely egy \(\displaystyle N\)-es dominókészlet összes pöttyeinek számát adja meg.

Egy nagy családban több gyereknek is van dominója, melyek játék közben összekeveredtek egymással.

Harmadik feladatként adjuk meg, hogy a dominók között melyek azok, amelyek többször fordulnak elő. A függvény bemenete a dominólapok nem rendezett listája, kimenete egy a fentiekhez hasonló rendezett lista.

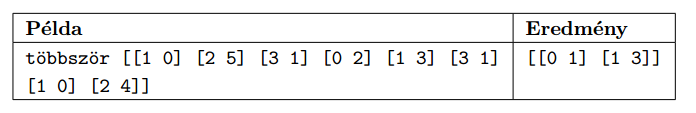
A megoldáshoz az Imagine Logo programozási környezetet ajánljuk, de a feladat megoldható Neumann-elvű programozási nyelvvel is (C, C++, Pascal, ...). A megoldás során - a be és kimenetektől eltekintve - csak a programozási nyelv funkcionális részét használjuk. Ne alkalmazzunk változókat, csak rekurzió segítségével valósítsunk meg az ismétlést. Igyekezzünk a megoldást minél több paraméterezhető függvényre bontani. A funkcionális programozásról az I. 259. feladatnál részletesen olvashatunk.

Beküldendő egy i289.zip tömörített állományban a megoldás forráskódja (i289.imp Imagine Logo Project, i289.pas, i289.cpp, ...) és egy i289.txt szöveges állomány, amely ismerteti a megoldás során készített függvényeket és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2012. április 10-én LEJÁRT.

Megoldásokról:

Elsősorban imagine, de visual basic, freepascal és c++ nyelvű megoldások is érkeztek. A funkcionális nyelvek, így a logo nyelv logikájának a rekurzív megoldási módszer elvárása testhez álló volt.

Állítsunk elő N méretű dominókészletet!

Példa: dominó 3 Eredmény: [[0 0] [0 1] [0 2] [0 3] [1 1] [1 2] [1 3] [2 2] [2 3] [3 3]]

Készítsünk függvényt, amely egy N nagyságú dominókészlet összes pöttyeinek számát adja meg!

Példa: pöttyszám 2 Eredmény: 12, pöttyszám 3 Eredmény: 30

Megjegyzés: az eredmény képlettel is kiszámítható: n(n+1)(n+2)/2.

Mintamegoldásként Fényes Balázs 9. osztályos (Budapest, Szerb Antal Gimnázium) tanuló visual basic nyelvű megoldását: i289.vb

és Kucsma Levente István 9. osztályos (Eger, Dobó István Gimnázium) tanuló imagine nyelvű: I289.IMP megoldását közöljük.

Statisztika:

11 dolgozat érkezett.
10 pontot kapott:	Fényes Balázs, Gema Barnabás, Kucsma Levente István, Szabó Levente, Tegzes Tamás, Varga 256 Erik.
9 pontot kapott:	Beleznay Soma, Kalló Kristóf.
6 pontot kapott:	3 versenyző.

A KöMaL 2012. márciusi informatika feladatai