 |
Az I. 329. feladat (2013. október) |
I. 329. Egy városnegyedben egyetlen teherautó végzi az üzletek közötti áruszállítást. A városnegyed Manhattan-szerű, mert csak egymásra merőleges utcái vannak.
Az üzletek címjegyzéke és példaként a teherautó egy lehetséges napi útvonala rendelkezésre állnak a honlapunkról elérhető szallitolevel.txt állományban. A címjegyzékben az üzletek sorszáma, a neve és a térkép-koordinátái vannak méterben. A napi útvonal egymás után tartalmazza az üzletek sorszámát. Lehet, hogy egy-egy üzletbe többször is szállítani kell, és a telephelyre is többször visszatérhet a teherautó.
Táblázatkezelő program segítségével oldjuk meg a következő feladatokat, amelyekkel statisztikai adatokat kapunk a napi szállításról:
A megoldás során vegyük figyelembe a következőket:
- Segédszámításokat az M oszloptól jobbra végezhetünk.
- Amennyiben lehetséges, a megoldás során képletet, függvényt, hivatkozást használjunk.
1. Töltsük be a tabulátorokkal tagolt, UTF-8 kódolású szallitolevel.txt szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. Munkánkat i329 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
Az A1:D34 tartományban az üzletek címjegyzéke van. Az F2-es cellától lefelé a napi szállításban egymás után felkeresendő üzletek sorszáma írható egymás alá. Ez utóbbiak listája naponta változhat. A teherautó napi útvonala maximum 30 elemből áll.
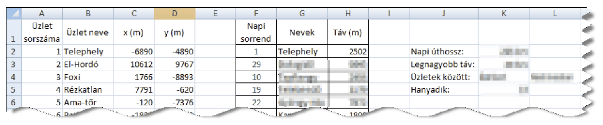
2. Segítsük a sofőr munkáját azzal, hogy a G2:G31 tartományban a szállítási címként szereplő üzletek nevét és a H2:H30 tartományban az egymás utáni üzletek távolságát határozzuk meg. Távolságon a feladatban a Manhattan-távolságot értjük. Az egyik üzlet (x1,y1) és valamely másik üzlet (x2,y2) Manhattan-távolsága |x1-x2|+|y1-y2|. Ha a ,,Napi sorrend''-ben üresen maradnak cellák, mert aznap harmincnál kevesebb fuvart kell lebonyolítani, akkor ezek sorában a nevek és a távolságok cellái is üresen jelenjenek meg.
3. A K2-es cellában számítsuk ki, hogy a teherautó hány kilométert tesz meg az adott napon. Az eredményül kapott összeget felfelé kerekítve, egészként, ,,km'' mértékegységgel jelenítsük meg.
4. A K3-as cellában határozzuk meg felfelé kerekítve kilométerben, hogy milyen távol van a napi útvonalban a két legtávolabbi üzlet. A K4-es és az L4-es cellában adjuk meg ennek a két üzletnek a nevét is.
5. A K5-ös cellában jelenítsük meg, hogy a leghosszabb útszakasz hányadik a napi útitervben.
6. A minta alapján végezzük el a szükséges cellaformázásokat.
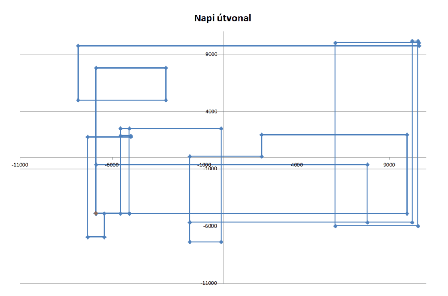
7. A teherautó napi útvonalát diagrammal tegyük szemléletessé. Az XY-diagramon jelenítsük meg az útvonalat úgy, hogy a merőleges fordulások pontjai is látszódjanak. A teherautó két üzlet között úgy közlekedik, hogy először x-irányban elmegy a megfelelő kereszteződésig, és onnantól erre merőleges irányban mozog tovább. A diagram rajzolását segédszámításokkal, segédkoordináták felvételével készítsük elő.
8. Az XY-diagramot külön munkalapra tegyük. Az üzletek és a fordulások helyét ábrázoló pontokat kössük össze. Egyéb beállítások:
- A diagramra ne tegyünk jelmagyarázatot.
- A diagram címe: ,,Napi útvonal''.
- A könnyebb értékleolvasás miatt a függőleges és vízszintes skálát  11000 méterig állítsuk.
11000 méterig állítsuk.
- Keressük meg a diagramon a ,,Telephely'' helyét ábrázoló pontot, és ennek színét állítsuk be a többitől eltérőre.
Beküldendő a táblázatkezelő munkafüzet (i329.xls, i329.ods, ...), illetve egy rövid dokumentáció (i329.txt, i329.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
Értékelés: az első hat feladat helyes megoldása 7 pontot, az utolsó két - az érettségi szintjét meghaladó feladat - megoldása 3 pontot ér.
Letölthető fájl: szallito.txt
(10 pont)
A beküldési határidő 2013. november 11-én LEJÁRT.
Megoldásokról:
A feladat első 6 része nem jelentett gondot a versenyzőknek. A napi úthossz meghatározásánál, figyelmetlenség miatt, néhányan a kilométerre történő átváltásról elfelejtkeztek. Ezt észrevehették volna, hiszen a km mértékegységet még a számok után meg is jelenítették. Ha a feladat tartalmán, a megoldás eredményén egy kicsit elgondolkoznak, akkor gyanús lehetett volna, hogy Föld egyenlítői hosszának hatszorosát talán egy teherautó egy nap nem teszi meg.
Ismét előkerült, hogy az egészre kerekítés és az egészre formázás nem ugyanaz. Az előbbit függvénnyel kell végezni (KEREK.FEL()), a másik megjelenítési beállítás.
A feladat újszerű része a diagramkészítésnél volt. A teherautók fordulási helyének koordinátáit segédcellákban meg kellett előre határozni. Észrevehetjük, hogy az üzletek x és y koordinátái felváltva változnak. A kiindulási Telephely után a páros sorokban változik az x és a páratlanokban az y. Például az 1. sor a kiindulási helyet jelöli, akkor a 2. sorban x irányban halad a teherautó és a 3.-ban y irányban, és így tovább.
Minta megoldás:
Kiss Ádám, 11. évfolyamos tanuló (Szeged, Radnóti Miklós Kísérleti Gimnázium és Általános Iskola) munkája: i329.ods
Statisztika:
19 dolgozat érkezett. 10 pontot kapott: Fehér Balázs, Fényes Balázs, Kiss 107 Ádám, Kovács Balázs Marcell. 9 pontot kapott: Csahók Tímea, Gercsó Márk, Mócsy Miklós, Németh 123 Balázs. 8 pontot kapott: 4 versenyző. 7 pontot kapott: 2 versenyző. 6 pontot kapott: 2 versenyző. 5 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2013. októberi informatika feladatai
|
|

