 |
Az I. 343. feladat (2014. március) |
I. 343. Egy N×N-es (1
N50) tábla cellái üres vagy színes négyzetek. A táblát függőlegesre állítva a színes négyzetek a legalacsonyabb üres helyet foglalják el, azaz a gravitáció miatt egymásra csúsznak. Háromféle: piros, kék és zöld színű négyzet lehetséges, amelyeket P, K és Z betűk jelölnek, az üres cellát a . karakter. A táblát szegély veszi körbe, ami megakadályozza, hogy a színes négyzetek kiessenek.
A táblát balra, jobbra, illetve függőlegesen át lehet forgatni. A forgatás hatására a színes négyzetek újra a legalacsonyabb szabad cellába csúsznak.
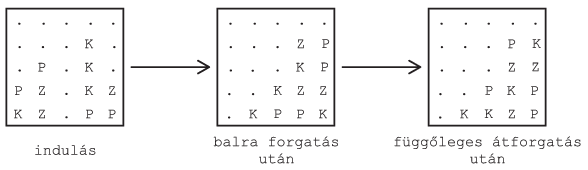
A tábla egyik oldalán egy nyílás van, amely induláskor a tábla legalsó sorának K-adik (1KN) oszlopába esik. Ezen keresztül a felette lévő színes négyzetek kicsúsznak, azaz a táblából törlődnek.
K=4 esetén:
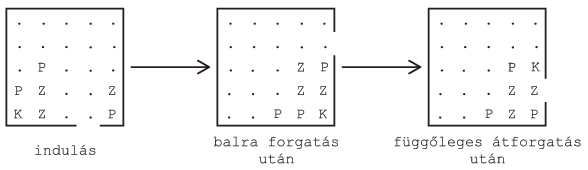
A tábla forgatását egy utasítássor adja meg. Az utasítássor B, J és F betűkből áll. A B a balra, a J jobbra és az F a függőleges átforgatást írja le.
Készítsünk programot i343 néven, amely a tábla forgatását leíró utasítássort végrehajtja.
A program első parancssori argumentuma a táblát és az utasítássort leíró adatállomány neve legyen. A fájl első sorában N (1N50) a tábla méretét és K (1KN) a nyílás helyét adja meg. Az ezt követő N sor a tábla indulás előtti cellánkénti tartalmát adja meg, majd a rákövetkező sorban a forgatásokat leíró utasítássor (1karakterek száma50) következik.
A parancssor második argumentumaként megadott kimeneti állomány első három sorába az utasítássor végrehajtása utáni színes négyzetek számát írjuk. Az ezt követő N sorba a tábla forgatások utáni állapotát adjuk meg cellánként.
Beküldendő a program forráskódja (i343.pas, i343.cpp, ...) és rövid dokumentációja (i343.txt, i343.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2014. április 10-én LEJÁRT.
Tesztállományok:
teszt1.be, teszt2.be, teszt3.be, teszt4.be, teszt5.be, teszt6.be és teszt7.be
Kimenetek: kimenetek.txt
Minta megoldás:
Csernák Tamás 12. osztályos tanuló (Fazekas Mihály Fővárosi Gyakorló Gimnázium, Budapest) megoldása: i343.pas
Uzonyi Ákos 8. osztályos tanuló (Szent Imre Gimnázium, Budapest) megoldása: I334.java
Statisztika:
15 dolgozat érkezett. 10 pontot kapott: Csernák Tamás, Kovács 246 Benedek, Uzonyi 000 Ákos. 9 pontot kapott: Szécsi Péter. 8 pontot kapott: 6 versenyző. 7 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző.
A KöMaL 2014. márciusi informatika feladatai