Az I. 378. feladat (2015. május)

I. 378. Adott egy \(\displaystyle N\times M\) pixelből álló fekete-fehér kép, amelyet táblázatos elrendezésben 0 és 1 számokkal írunk le. Egy ilyen képet akkor tekintünk szépnek, ha az élszomszédos mezők közül minél több azonos. Célunk az eredeti kép szebbé alakítása bizonyos pixelek értékének megcserélésével. Egy képpont cseréje \(\displaystyle Q\) forintba kerül. Az átalakított kép szépségét úgy vesszük figyelembe, hogy minden élszomszédos, különböző színű pixelpár további \(\displaystyle P\) forint ,,költséget'' jelent. Keressük meg néhány adott képre azt az átalakítást, amely mellett a lehető legkisebb a \(\displaystyle P+Q\) költség.

Programot nem kell beküldeni, egyedül a három, honlapunkról letölthető (in.1, in.2, in.3) képre kell három kimenetet adni (out.1, out.2, out.3). A bemenet első sorában négy egész szám áll: \(\displaystyle N\), \(\displaystyle M\), \(\displaystyle P\), \(\displaystyle Q\) -- a táblázat sorainak, oszlopainak száma, illetve a két költséget leíró paraméter. Ezután \(\displaystyle N\) sor következik, mindegyikben \(\displaystyle M\) karakter: a fénykép. A kimenet szintén egy \(\displaystyle N\times M\)-es táblázat a bemenethez hasonló formában. A feladatra nem feltétlenül kell optimális megoldást adni, mivel a feladat beküldői egymással versenyeznek: az kap 10 pontot, akinek a három bemenetre összesen a legkisebb a \(\displaystyle P+Q\) költség, a többiek arányosan kevesebbet. Például a következő kép esetén:

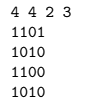
egy lehetséges (nem feltétlenül optimális) átalakítás:

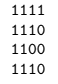
Itt \(\displaystyle 6\cdot 2+3\cdot 3 =21\) forint a költség.

Beküldendő a három átalakított fénykép egy tömörített (i378.zip) állományban.

Letöltendő állományok: in.1, in.2, in.3.

(10 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Statisztika:

6 dolgozat érkezett.
10 pontot kapott:	Gercsó Márk.
9 pontot kapott:	Kovács 246 Benedek.
8 pontot kapott:	1 versenyző.
7 pontot kapott:	1 versenyző.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.

A KöMaL 2015. májusi informatika feladatai