Az I. 382. feladat (2015. október)

I. 382. A ZUMA egy többféle elrendezésű pályán játszott lövöldözős játék. A játék során a pályán mozgó, kezdetben folytonos sort alkotó, különböző színű golyókat kell lövések segítségével eltüntetni, mielőtt azok bármelyike elérné a pálya végét. Készítsünk programot, amelyben a játékot egy egyenes szakaszon játsszuk, a golyók balról jobbra mozognak és minden időegységben egy lövés történik.

Szabályok:

\(\displaystyle \bullet\) a golyók kezdetben a pálya bal oldalán helyezkednek el, közöttük golyó nélküli pozíció nincs;

\(\displaystyle \bullet\) balról az első golyó minden időegységben egy egységgel tolódik jobbra;

\(\displaystyle \bullet\) minden olyan golyó tolódik, amelynek a szomszédja tolódik;

\(\displaystyle \bullet\) a kilőtt golyó tolódás után ér célba, de még ugyanabban az időegységben

\(\displaystyle \circ\) ha a találat helyén golyó van, akkor

\(\displaystyle *\) ha a találat helyén és közvetlenül mellette azonos színű golyók voltak egymás mellett;

- azokat eltünteti, helyük üres lesz;

- amíg az üressé váló rész két oldalán együttvéve 3 vagy több azonos színű golyó van, azok is eltűnnek;

\(\displaystyle *\) különben a kilőtt golyó a találat helyére kerül, az ott lévő golyó pedig jobbra tolódik és a jobbra lévő golyók közül mindazok tolódnak, amelyek szomszédja tolódik;

\(\displaystyle \circ\) ha a találat helyén nincs golyó, akkor

\(\displaystyle *\) ha valamely szomszédjában van golyó, a golyó a célhelyen marad;

\(\displaystyle *\) különben a golyó eltűnik.

A bemeneti fájl első sora a pálya \(\displaystyle h\) hosszát, a pályán lévő golyók \(\displaystyle p\) számát és a játék során kilőtt golyók \(\displaystyle k\) számát tartalmazza. A második sor \(\displaystyle p\) darab karaktert tartalmaz, amely a golyók színét jelöli, amelyek sorrendben a pálya bal szélétől helyezkednek el. (A golyók színét az A, ..., F karakterek jelölik.) A következő \(\displaystyle k\) sor egy-egy golyó-hely párt tartalmaz: a páros első tagja a golyó színét jelöli, a második tagja pedig a pozíciót, amelyen a golyó a pályát eléri. A kimenet a rendszer állapotát mutatja az utolsó lövést követően.

\(\displaystyle \bullet\) Ha az összes golyót sikerült lövésekkel eltüntetni, akkor az első sorba 0 kerüljön, a második sorba azon lövés sorszáma, amely után ez először teljesült.

\(\displaystyle \bullet\) Ha valamely golyó elérte a pálya végét, akkor az első sorba a -1 kerüljön, a második sorba pedig azon lövés sorszáma, amely után ez történt.

\(\displaystyle \bullet\) Ha van még golyó a pályán, de egy sem érte el a végét, akkor az első sor az 1 értéket tartalmazza, a második sor pedig \(\displaystyle h\) darab karaktert, amely a pályán lévő golyók színét jelöli balról jobbra. Az üres pozíciókra . kerüljön.

Az alábbi példa sorai egy-egy, egymástól független állapotokban bekövetkezett lövést és annak eredményét mutatják.

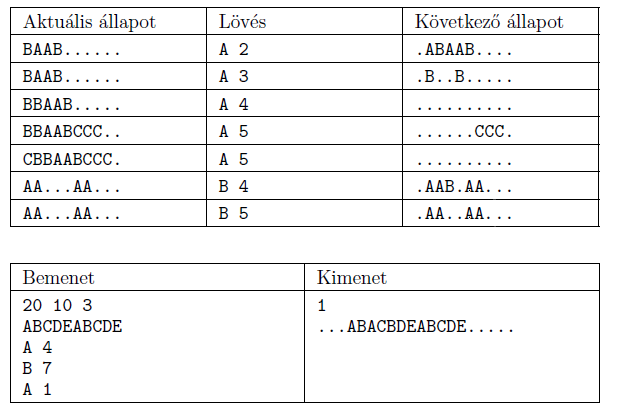
A program első parancssori argumentuma a bemeneti fájl neve, a második pedig a kimeneti fájl neve legyen.

Beküldendő egy tömörített i382.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2015. november 10-én LEJÁRT.

A megoldások értékeléséhez a következő bemeneteket használtuk: i382bemenet.zip

be0a-0e: a feladatleírásnál megadott eseteket tartalmazza (3 helyes - 1 pont, 5 helyes - 2 pont)

be0f-0g: azonos elemekre vonatkozó speciális eset (mindkettő helyes: 1 pont)

be1a-1b: azonos elemekre vonatkozó speciális eset (mindkettő helyes: 1 pont)

be2: a feladatleírásban megtalálható minta

be3-be5: általános tesztesetek

Az érdemi dokumentáció 1 pontot ért, a bemenetek leírásnak megfelelő kezelése újabb 1 pontot jelentett.

Statisztika:

10 dolgozat érkezett.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	2 versenyző.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2015. októberi informatika feladatai