Az I. 388. feladat (2015. december)

I. 388. Ma már mindenki számára megszokott, hogy a térképek északi tájolásúak, de ez alig néhány száz éve van így. Korábban az adott kultúrkörnek megfelelő irányt használtak. Az egyiptomiak a Nílus folyásirányát, az amerikai telepesek a vándorlás irányát (nyugat), az európaiak pedig északot.

Ebben a feladatban csak olyan térképeket használunk, amelyek a négy fő égtáj valamelyike szerint tájoltak. A feladatban szereplő térképek más és más céllal készültek, más és más nevezetes pontok szerepelnek rajtuk. Ezen pontok koordinátáinak ismeretében kell megállapítanunk az egyes térképek tájolását. A térképeken az origó más és más pontban lehet.

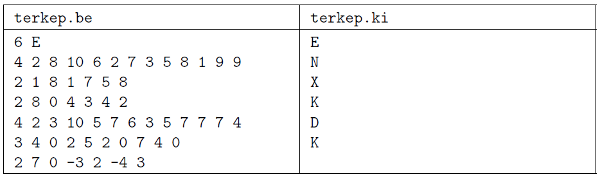
A bemeneti fájl első sora tartalmazza a térképek (\(\displaystyle T\le 50\)) számát és attól egy szóközzel elválasztva az első térkép tájolását (E, K, D, N). A következő \(\displaystyle T\) sor mindegyikében az első szám az adott térképen szereplő pontok (\(\displaystyle N\)) számát adja meg. Ezt követően \(\displaystyle N\) számhármas szerepel, amelyből az első szám a pont sorszáma, utána pedig annak \(\displaystyle X\) és \(\displaystyle Y\) koordinátája az adott térképen. A soron belüli határoló jel a szóköz. A pontok száma összességében legfeljebb 50. A koordináták értéke a \(\displaystyle [-1000; 1000]\) intervallumban van az adott tájolású térképen, de a különböző térképek egyesítésével az intervallum megnőhet.

A kimeneti fájl pontosan \(\displaystyle N\) sort tartalmazzon, amelyben soronként egy karakter, a térkép tájolása álljon. Ha a tájolás nem állapítható meg, akkor a sorban az X karakter szerepeljen.

Beküldendő egy tömörített i388.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás vázlatos leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Az értékeléshez használt bemeneti fájlok: i388bemenet.zip

0. a feladatleírásban használt mintabemenet

1. mindegyik azonos állású, az origó azonos

2. mindegyik azonos állású, az origó változik

3. azonosan irányított, nagy méret

4-7. különböző méretű általános tesztesetek

Mindegyik teszteset helyes megoldása 1-1 pontot ér.

Mintaként Olexó Gergely megoldását adjuk közre: OGi388.zip

Statisztika:

6 dolgozat érkezett.
10 pontot kapott:	Nagy Ábel, Olexó Gergely.
9 pontot kapott:	Kovács 246 Benedek, Szakali Benedek.
7 pontot kapott:	2 versenyző.

A KöMaL 2015. decemberi informatika feladatai