Az I. 389. feladat (2015. december)

I. 389. Az atlétika női versenyei közül a legösszetettebb a hétpróba. Ezzel foglalkozó adatbázis-kezelési feladat volt az I. 338-as. Egy verseny eredményeinek kiértékelését most táblázatkezelővel végezzük el.

A hétpróba hét versenyszáma: 100 m gátfutás, 200 m és 800 m futás, magasugrás, távolugrás, súlylökés és gerelyhajítás. A verseny pontozásos rendszerű. A versenyszámokat nemzetközi ponttáblázat alapján értékelik, amelyben minden elért eredménynek megvan a maga pontszáma.

A versenyszám pontszámának kiszámítására a következő képletet használják a versenyző \(\displaystyle X\) eredményét figyelembe véve:

\(\displaystyle \text{pont}=\big[A\cdot {|X-B|}^C\big] \)

(ahol \(\displaystyle [~]\) a kifejezés egészrészét, \(\displaystyle |~|\) az abszolút értékét jelenti).

Az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) konstansok a Nemzetközi Atlétikai Szövetség által közölt, versenyszámonként eltérő konstansok.

A 2012. évi nyári olimpiai játékok hétpróba verseny adatait és az előző táblázatban lévő konstansokat rögzítettük a hetforras.txt tabulátorral tagolt, UTF-8 kódolású állományban.

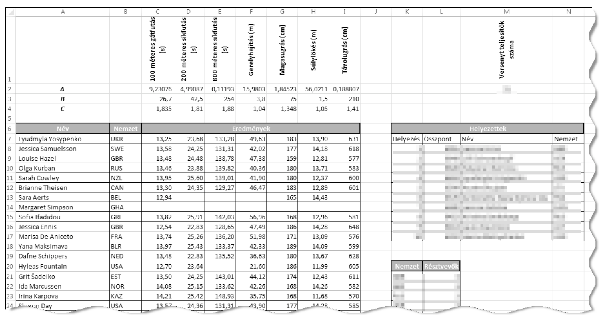
1. Töltsük be a hetforras.txt szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. (Az A1:I4 tartományban a fenti táblázat transzponált változata található.) A munkalap neve legyen eredmények. Munkánkat hetproba néven mentsük el a táblázatkezelő alapértelmezett formátumában.

2. Hozzunk létre új munkalapot pontszámok néven, és a minta szerinti fejlécet alakítsuk ki az első sorban.

3. Ezen a munkalapon az A2:B40 cellákban - az eredmények munkalap A7:B45 celláira hivatkozva - jelenítsük meg a 39 versenyző nevét és nemzetiségét.

4. A C2:I40 cellákban, a fent megadott számítási módszer szerint, egyetlen képlettel és annak másolásával határozzuk meg a versenyzők versenyszámonként elért pontszámát. Ha a versenyeredmény cella üres, akkor a kifejezés szerint az erre hivatkozó pontszám cellája is legyen üres.

5. A J2:J40 cellákban adjuk meg a versenyzők versenyszámonként elért pontszámainak összegét, ha mind a hét versenyszámból pontszámmal rendelkeznek, különben a ,,Nincs'' felirat jelenjen meg.

A következő feladatokat az eredmények munkalapon végezzük el.

6. Az M2 cellában határozzuk meg függvény segítségével a versenyt teljesítők számát. A versenyt az teljesítette, aki mind a hét versenyszámban pontokat szerzett.

7. A K8:N17 cellákban képlettel adjuk meg az első tíz helyezett versenyző pontszámát, nevét és nemzetiségének rövidítését. A hétpróba győztese a legtöbb pontot elérő versenyző (feltételezhetjük, hogy azonos pontszámokat nem értek el a versenyzők).

8. A C50:I50 cellákban határozzuk meg a versenyszámonkénti győztesek nevét. Azonos eredmények esetén elegendő egyikőjük nevét megadnunk.

9. A hétpróba versenyen nemzetenként többen is részt vehetnek. A K20:L20 cella alatt soroljuk fel a versenyzők száma szerint csökkenő sorrendben, hogy az egyes nemzetekből hány induló volt. A megoldásban a K oszlopban nem szükséges a képletek használata, megfelelő a nemzetek hárombetűs rövidítésének kigyűjtése is.

10. Az eredmények munkalap celláit formázzuk a minta szerint.

Beküldendő egy tömörített i389.zip állományban a munkafüzet (hetproba.xlsx, hetproba.odt), valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott táblázatkezelő neve és verziószáma.

Letölthető fájl: hetforras.txt

(10 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Megoldásokról:

Két feladat volt, amit többen eltévesztettek. A 7.e-t nem, amelynek a szövege a következő volt:

A K8:N17 cellákban képlettel adjuk meg az első tíz helyezett versenyző pontszámát, nevét és nemzetiségének rövidítését.

A megoldásokban az első tíz helyezett nevét többen nem képlettel határozták meg, hanem rendezéssel, amely pontszám változás esetén nem frissül. Egy lehetséges megoldás a =NAGY() függvény használata.

A 8. feladatra is több téves megoldás érkezett. A futás számoknál, nem a maximális idejűek a győztesek természetesen. (A dobó számoknál természetesen a maximális távolságot elérőek nyertek.) Helyesen a pontszámok maximumát kellett volna vizsgálni.

Minta megoldás:

Pécz Bálint 11. osztályos tanuló (Budapesti Németh László Gimnázium, Budapest) megoldása: hetproba.xlsx

Statisztika:

11 dolgozat érkezett.
10 pontot kapott:	Kovács 246 Benedek, Nagy Ábel, Németh 729 Gábor, Olexó Gergely, Pécz Bálint, Szakali Benedek.
9 pontot kapott:	Kelkó Balázs.
8 pontot kapott:	1 versenyző.
7 pontot kapott:	2 versenyző.
3 pontot kapott:	1 versenyző.

A KöMaL 2015. decemberi informatika feladatai