 |
Az I. 393. feladat (2016. január) |
I. 393. A GeoGebra program széles körben használható matematikai fogalmak, függvény-transzformációk, geometriai szerkesztések stb. szemléltetésére. Egy látványos felhasználása lehet például a szögfüggvények ábrázolása, ahol a forgó egységvektor megfelelő koordinátáiból alakul ki a függvény.
Készítsünk GeoGebra munkalapot a tangens függvény származtatásának szemléltetésére a függvény definíciója alapján az alábbiak szerint:
A munkalapon jelenjen meg egy kör és egy koordináta-rendszer úgy, hogy a koordináta-rendszer x tengelyének egyenese menjen át a kör középpontján, a koordináta-rendszerben pedig az egység a kör sugara legyen.
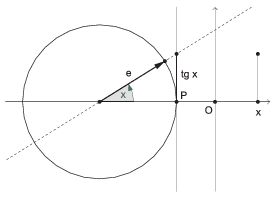
Mint az ábráról leolvasható, a szög tangensét az egységvektor egyenesének meghosszabbítása metszi ki a kör P pontjába állított érintőből (lásd az ábrát). A körben forogjon körbe az e egységvektor, és a szögértékek egyenletes változása mellett a szöghöz tartozó tangens értéket szemléltető szakasz (lehetőleg animációval) ússzon át az érintőről a koordináta-rendszerbe a szögnek megfelelő x értékhez.
A koordináta-rendszerben a fenti lépések alapján folyamatosan bővülve jelenjen meg a tangens függvény grafikonja. A felhasználónak adjunk lehetőséget arra, hogy csúszka segítségével beállíthassa a mintavételezés szögét (sűrűségét).
A megjelenő ábrának legalább a ]−π/2,3π/2[ intervallumot tartalmaznia kell.
Beküldendő egy i393.zip tömörített állományban a GeoGebra munkalap és dokumentációja, amely tartalmazza a megoldás rövid leírását.
(10 pont)
A beküldési határidő 2016. február 10-én LEJÁRT.
A megoldásokról: A feladatra érkezett megoldások mindegyike az előírt módon jeleníti meg a tangens függvényt. Egy esetben hiányzott a mintavételezés beállításához előírt csúszka. Több megoldó törekedett látványos elemek "belecsempészésére" is, pl. oszcilláló animáció, az érintőről induló pontok egyenletes sebességgel való mozgatása.
A közölt minta megoldás: A minta megoldás Kovács 246 Benedektől a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulójától származik, aki listák segítségével dolgozott.
Statisztika:
6 dolgozat érkezett. 10 pontot kapott: Kovács 246 Benedek, Nagy Ábel, Olexó Gergely, Szakali Benedek, Szemerédi Levente. 9 pontot kapott: Rittgasszer Ákos.
A KöMaL 2016. januári informatika feladatai
|
|

