Az I. 400. feladat (2016. április)

I. 400. Egy \(\displaystyle N\times M\) (\(\displaystyle 10\le N,M\le 10\,000\)) téglalap alakú területen \(\displaystyle K\) (\(\displaystyle 0\le K\le 1\,000\)) darab különböző szélességű és hosszúságú téglalap elszórtan helyezkedik el. A téglalapok oldalai párhuzamosak a terület oldalaival, érintkezhetnek és átfedhetik egymást, de a területről nem nyúlhatnak ki.

Készítsünk programot i400 néven, amely a következő problémákat oldja meg.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et, \(\displaystyle M\)-et és \(\displaystyle K\)-t, majd a következő \(\displaystyle K\) sorból a téglalapok bal felső, illetve jobb alsó sarkainak \(\displaystyle X\) és \(\displaystyle Y\) koordinátáit (egész számok).

A program írja a standard outputra a kérdésekre adott válaszokat soronként:

- soroljuk fel a beolvasás sorrendjében azoknak a téglalapoknak a sorszámát, amelyek a terület határához hozzáérnek;

- adjuk meg, hogy melyik az a téglalap, amelyik a legtöbb más téglalap valamelyik csúcsát tartalmazza; a számításnál az érintkezést ne vegyük figyelembe, több azonos téglalap esetén elegendő egyet megadni;

- adjuk meg, hogy hány olyan téglalap van, amely a többitől független, azaz nem ér egyetlen másik téglalaphoz sem, nem metszi, nem tartalmaz egy másikat sem, illetve őt sem tartalmazzák.

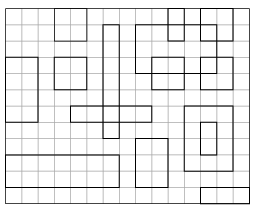
Példa (amelyben az újsor karakterek egy részét a tömörség kedvéért / jellel helyettesítettük):

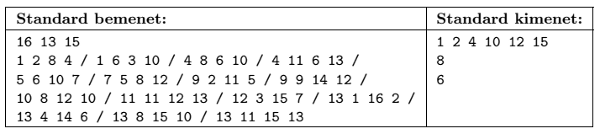
Beküldendő egy tömörített i400.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2016. május 10-én LEJÁRT.

Mintamegoldás és értelmezés:

Szakali Benedek 10. osztályos tanuló Kecskemét, Kecskeméti Bányai Júlia Gimnázium megoldása: main.cpp

A terület határához érőket úgy szűrtem ki, hogy megvizsgáltam, van-e olyan koordinátájuk, ami a minimum vagy maximum értéket veszi fel.

A második feladatnál egy téglalap akkor tartalmaz egy csúcsot, ha a csúcs mindkét koordinátája a téglalap határain belül van.

A harmadik feladatnál azokat az eseteket vizsgáltam meg, amikor a másik téglalap nem lép kapcsolatba az éppen vizsgálttal. Ez akkor van így, ha a másik téglalap legkisebb x vagy y koordinátája is nagyobb, mint az éppen vizsgált téglalap legnagyobbja, illetve a másik téglalap legnagyobb x vagy y koordinátája is kisebb, mint az éppen vizsgált legkisebbje. Ha a vizsgálat hamis eredményt ad vissza, az éppen aktuális téglalap már nem lehet független.

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Hamrik Szabin, Kovács 246 Benedek, Nagy Ábel, Olexó Gergely, Szakali Benedek.
6 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2016. áprilisi informatika feladatai