Az I. 411. feladat (2016. október)

I. 411. Folyadékok síkbeli modellezésére diffúziós keretmodellt használhatunk. Ennek a lényege: legyen \(\displaystyle T[N,M]\) kétdimenziós táblázat kétféle számmal \(\displaystyle (0,1)\) véletlenszerűen feltöltve. Az 1 a molekulát és a 0 az üres helyet jelenti. A táblázat egy-egy véletlenszerűen kiválasztott molekulájával elemi esemény történhet, amelyet a Szimulációs lépés eljárással adunk meg.

Ha a \(\displaystyle T\) táblázat egy véletlenszerűen kiválasztott molekuláját annak szintén véletlenszerűen kiválasztott szomszédjával megcseréljük, akkor ennek az elemi műveletnek a nagyszámú ismételt végrehajtásával a gázok diffúzióját szimuláljuk. Ezt a modellt bővítjük a molekulák rövidtávú vonzásával, így a síkbeli folyadékmodellhez jutunk.

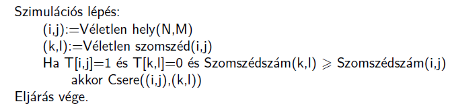
A Véletlen hely() függvény a \(\displaystyle T\) táblázat egy véletlenszerűen kiválasztott cellájának indexeit adja meg. A Véletlen szomszéd() függvény a paraméterként kapott cella véletlenszerű szomszédjának indexeit adja vissza. Lényeges, hogy ne válasszon a táblázaton kívüli helyet. A Csere() eljárás a paraméterként kapott két cella tartalmát cseréli meg.

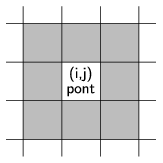
A Szomszédszám() eljárás a paraméterként kapott hely közvetlen szomszédjainak molekulaszámát határozza meg.

Egyszerűbb módszert is készíthetünk a szomszédválasztásra (Véletlen szomszéd()), ha a \(\displaystyle T\) táblázatunkat körülvesszük fallal, 0-kal, amely nem hat a molekulák mozgására. Így a szomszédot a falban is választhatjuk, ha még egy külső falat hozunk létre pl. \(\displaystyle -10\) értékekkel.

Készítsünk programot i411 néven, amely parancssori vagy grafikus felületen a folyadékok síkbeli modelljét bemutatja tetszőlegesen választott \(\displaystyle N\) és \(\displaystyle M\) értékekre.

A programban két beavatkozási lehetőség legyen: Megállítás/Folytatás és Kilépés.

Beküldendő egy tömörített i411.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2016. november 10-én LEJÁRT.

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:	Bodgál Attila Zoltán, Kis Lázár Bence, Szakali Benedek.
9 pontot kapott:	Rittgasszer Ákos.
8 pontot kapott:	1 versenyző.
5 pontot kapott:	2 versenyző.
4 pontot kapott:	1 versenyző.

A KöMaL 2016. októberi informatika feladatai