 |
Az I. 451. feladat (2018. március) |
I. 451. Kukac-robot egy számsoron szeretne végighaladni, végigkúszni. A robot onnan kapta a nevét, hogy mozgása a kukacokéra emlékeztet. A kúszás két fázisból áll: először összehúzza magát úgy, hogy testének első része helyben marad a számsoron és a végét előre húzza, amíg csak lehet; majd másodszor fordítva, testének utolsó pontja marad egy helyben és előre kinyúlik, amíg a szabályok engedik.
Szabályok:
– Összehúzott állapotban a Kukac-robot alatt lévő számok összege legalább \(\displaystyle K\), és a lefedett számok száma kettőnél nem lehet kevesebb.
– Kinyújtott állapotban legfeljebb \(\displaystyle L\) lehet az alatta levő számok összege és nem nyúlhat öt számnál hosszabban.
– A Kukac-robot induló helyzete: az első két számon helyezkedik el összehúzott állapotban. (A kezdőállapotra a szabályokat nem kell vizsgálni.)
– Beérkezésnek számít az a kinyújtott állapot, amikor a számsor utolsó tagját lefedi.
Készítsünk programot i451 néven, amely meghatározza, hogy Kukac-robot végig tud-e menni a számsoron és ha igen, akkor legkevesebb hány lépésben.
A program standard bemenetének első sorában 3 szám van: \(\displaystyle N\) (\(\displaystyle 10\le N\le 10\,000\)) a számsor hossza, \(\displaystyle K\) (\(\displaystyle 2\le K\le 20\)) összehúzott állapotban a Kukac-robot alatti és \(\displaystyle L\) (\(\displaystyle K<L\le 45\)) a kinyújtott állapot alatti számok összege. Az ezt követő sorban a számsor tagjait adjuk meg szóközzel elválasztva, azaz \(\displaystyle N\) darab számot \(\displaystyle x_{i}\) (\(\displaystyle 0\le x_{i} \le 9)\).
A program írja ki a standard kimenetre, hogy legkevesebb hány megnyúlás alatt kúszik át a Kukac-robot a számsoron. Ha nem tud a számsoron végigkúszni, akkor a kimenet legyen -1.
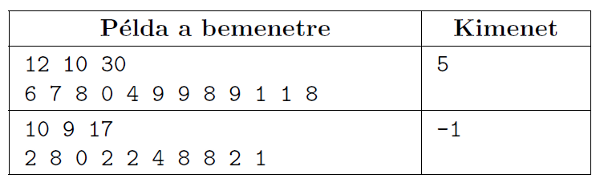
Beküldendő egy tömörített i451.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2018. április 10-én LEJÁRT.
Tesztállományok:
Statisztika:
11 dolgozat érkezett. 10 pontot kapott: Békési Péter, Horcsin Bálint, Szalay Bálint, Ürmössy Dorottya, Vígh Márton. 9 pontot kapott: Bálint Ádám, Katkó Dominik, Zsombó István. 8 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2018. márciusi informatika feladatai