Az I. 463. feladat (2018. október)

I. 463. (É). Adott egy nagyméretű négyzethálós lap, amelynek \(\displaystyle O\) oszlopa és \(\displaystyle S\) sora van. A négyzetek csúcspontjainak koordinátái egész számok, a bal alsó sarok az origó, azaz a \(\displaystyle (0;0)\) koordinátájú pont. A lapon egy szikével bemetszéseket készítünk, amelyek párhuzamosak a lap valamelyik oldalával. A bemetszések végpontjai egész koordinátájú pontok. Tudjuk, hogy bemetszés nem indul és nem végződik a lap szélén.

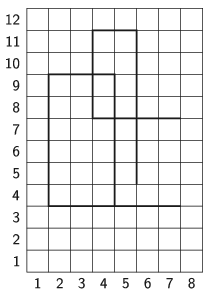
A honlapunkról letölthető nhalo.txt szöveges állomány első sorában a négyzetháló méretét megadó \(\displaystyle O\) és \(\displaystyle S\) értékek találhatók. A következő sorban a bemetszések \(\displaystyle B\) száma szerepel. Az ezt követő \(\displaystyle B\) sor mindegyikében egy számnégyes található, amelyből az első számpár a bevágás egyik végpontja, a második pedig a bevágás másik végpontja. A számpárok első tagja az oszlop, a második a sor koordinátája. A számokat pontosan egy szóköz választja el egymástól, a számok egyike sem nagyobb, mint 1000.

Készítsünk programot, amely a lap méretének és a bemetszések adatainak ismeretében megoldja a következő feladatokat. Minden feladat megoldása előtt írjuk ki a feladat sorszámát, pl. ,,1. feladat:'', illetve a beolvasás és kiírás esetén röviden írjunk magyarázó szöveget. Az ékezetmentes kiírás is elfogadott.

1. feladat: Olvassuk be a szöveges állományból az adatokat, és tároljuk el későbbi feldolgozás céljából.

2. feladat: Írjuk ki a legkisebb sorszámú sort, amelyben nincs bemetszés, például a következő formában: ,,A legkisebb sorszámú bemetszés nélküli sor: 2''.

3. feladat: Adjuk meg annak a legkisebb téglalapnak a területét, amely az összes bemetszést tartalmazza. A kimenet például ,,A legkisebb, minden bemetszést tartalmazó téglalap területe: 48''.

4. feladat: Adjuk meg, hogy összesen hány pontban találkoznak merőlegesen bemetszések. A kimenet például ,,A metszések 10 helyen találkoznak merőlegesen''.

5. feladat: Kérjünk be a felhasználótól egy oszlopszámot, és adjuk meg, hogy az adott oszlop milyen hosszúságú része nem tartalmaz bemetszést.

6. feladat: Adjuk meg a bemetszések hosszának átlagát két tizedesjegy pontossággal megjelenítve, például ,,A metszések átlagos hossza 4,75''.

7. feladat (ez a részfeladat az emelt szintű érettségi programozási feladatoknál összetettebb, nehezebb): Hozzuk létre a sorok.txt szöveges állományt, amely a négyzetháló bemetszések utáni helyzetét mutatja a sorok szerint. A szöveges állomány \(\displaystyle S\) sort tartalmaz, elsőként a négyzetháló legfelső egységnégyzeteit, majd sorban az utána következő négyzeteket, végül a négyzetháló legalsó sorának négyzeteit írja le. Ha egy sorban nincs függőleges bemetszés, akkor abban csak a 0 szám szerepel. Egyébként annyi egész van benne, ahány függőleges bemetszést ejtettek a sorban. Ilyenkor az egészek oszlopok szerint növekvő sorrendben mutatják a sor összefüggő, nem szétvágott négyzeteinek számát.

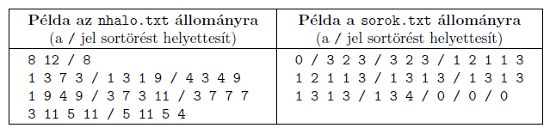
Beküldendő egy i463.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

Letölthető állomány: nhalo.txt

(10 pont)

A beküldési határidő 2018. november 12-én LEJÁRT.

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Ürmössy Dorottya, Zámborszky Balázs.
9 pontot kapott:	Bálint Ádám, Békési Péter, Nagy 793 Márton.
8 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2018. októberi informatika feladatai